Euclide Geometry Problem

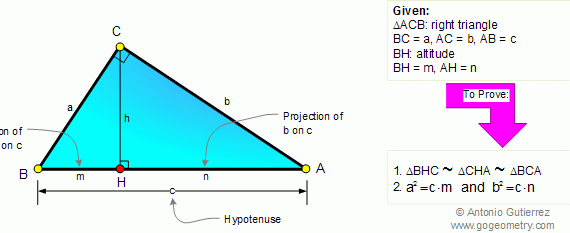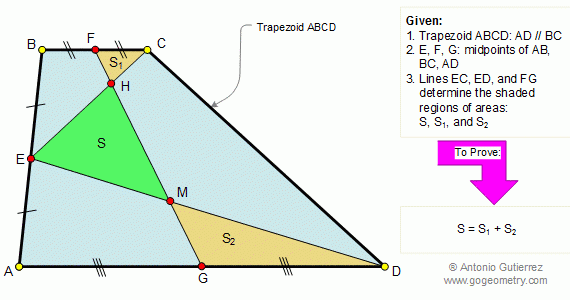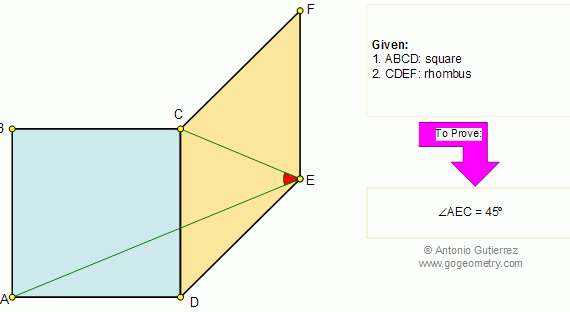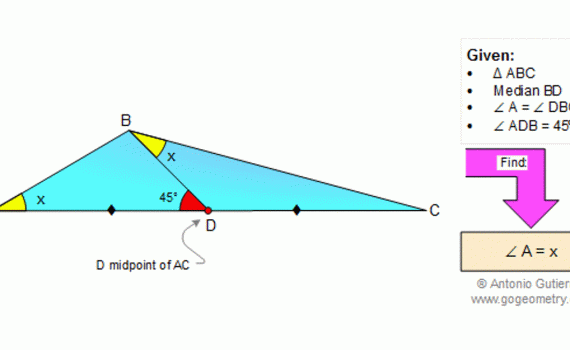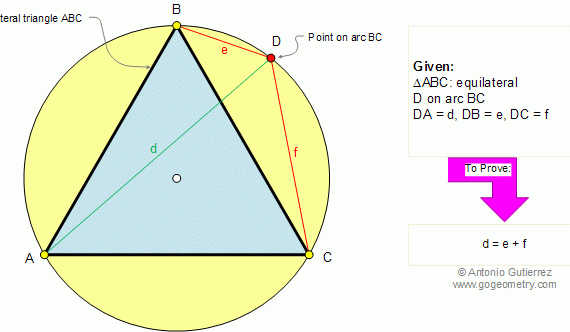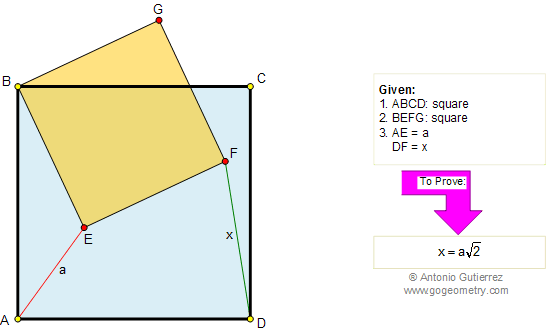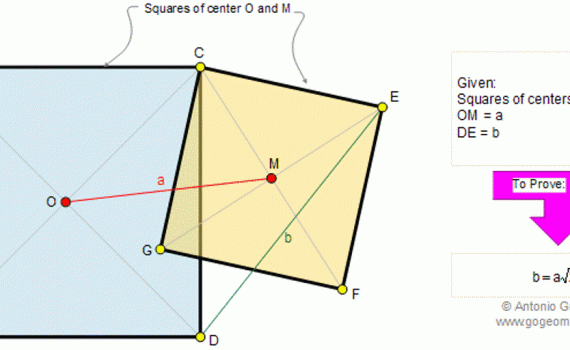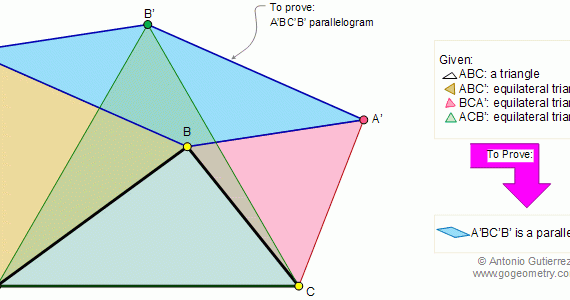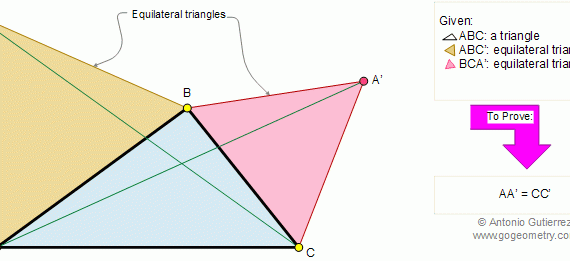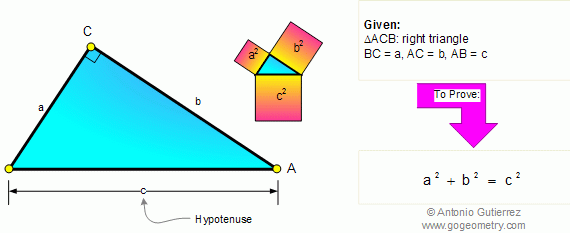
From Gogeometry Using : Isometric transformation Additional points congruent triangles Area of a triangle Define a square ABCD Define E in AB, AE=a and EB=b Define F in BC such as BF=b and FC=a [ABCD]=[HIGD]+[EBFI]+[AEIH]+[FCGI] [AEIH]=[FCGI]=ab=>[ABCD]=a^2+b^2+2ab=(a+b)^2 Cut [AEIH] in 2 triangles T1=AEI and T2=AHI Cut [FCGI] in 2 triangles T3=FCG […]

Pythagoras theorem

 dans Euclide Geometry Principles / Euclide Geometry Problem par
From Gogeometry Using : Pythagoras Similar triangles In ΔBHC : ∠ABC + ∠HCB =90° In ΔBCA : ∠HCA + ∠HCB =90° => ∠HCA = ∠ABC=β In ΔCHA : ∠HCA +∠BAC=90° => ∠HCB =∠BAC= α => ΔBHC is similar to ΔCHA (aaa=β90α) and ΔBHC is similar to ΔBCA (aaa=β90α) Therefore ΔBHC, […]

Gogeometry Problem 264

 dans Euclide Geometry Problem par
From Gogeometry Using : Additional points Thales theorem Area of a triangle   Define S0=[ABCD], L midpoint of CD, I intersection of AB and CD and h the height of CBE and DAE [ECL]=EL*h/2 and [ELD]=EL*h/2 => [ECD]=EL*h [BCE]=BC*h/2 and [AED]=AD*h/2 EL=(BC+AD)/2 S0=[ECD]+[BCE]+[AED]=EL*h + (BC+AD)*h/2= EL*h + EL*h => [ECD]=[BCE]+[AED]=S0/2 […]

Problem 171

 dans Euclide Geometry Problem par
From Gogeometry Using : central and inscribed angle   CDEF Rombus =>DC=DE ABCD square =>DC=DA DA=DC=DE => A, C and E are on the circle with center D and radius AD With the theorem of inscribed angle, « the central angle of a circle is twice any inscribed angle” : <ADC=2<CEA […]

Gogeometry Problem 179

 dans Euclide Geometry Problem par
From Gogeometry   Using : Isometric transformation Additional points Pythagoras congruent triangles Equilateral triangle Let b=AD=DC and d=BC ∠BAC= ∠CBD and ∠BCD= ∠BCA => ΔCAB is similar to ΔCBD =>AC/BC=CB/CD=AB/BD => 2b^2=d^2, which means that d is the hypothenuse of a right triangle with side b Define C’ such as […]

Gogeometry Problem 1

 dans Euclide Geometry Problem par
From Gogeometry   Using : Additional points Inscribed angles in a circle congruent triangles Equilateral triangle CAD intercepts arc CD such as CBD => ∠CAD= ∠CBD Define D’ n AD such as AD’C is congruent to BDC => AD’=f and ∠ACD’= ∠BCD ∠ACD= ∠ACB+ ∠BCD=Π/3+ ∠BCD And ∠ACD= ∠ACD’+ ∠D’CD=∠BCD+ […]

Gogeometry Problem 256

 dans Euclide Geometry Problem par
From Gogeometry : Using : Congruent triangles Isometric transformation Additional points Pythagoras BGC is congruent to BEA (by rotation of PI/2) BA⊥BC, BE⊥BG => AE⊥CG   Define H such as AHD is the translation of BGC AHD is congruent to BGC (by translation) => BG=AH=EF and BG//AH//EF AE⊥CG, DH//CG => […]

Gogeometry Problem 189

 dans Euclide Geometry Problem par
From Gogeometry :   Using : isometric transformation additional point Pythagoras Define H such as ΔHOB is the rotation of ΔMOC of -Π => OM ⊥ OH, OM=OH=a, MC ⊥ HB MC ⊥ ME, MC ⊥ HB => ME // HB Hence MEBH is a parallelogram => HM=BE=b => b […]

Gogeometry Problem 244

 dans Euclide Geometry Problem par
From Gogeomety     Using : Equilateral triangle Congruent triangles Parallelogram ΔACB’ and ΔBCA’ are equilateral => ∠ACB’ =∠BCA’ = Π/3 ∠ACB = ∠ACB’ – ∠B’CB = Π/3 – ∠B’CB ∠B’CA’ = ∠BCA’ – ∠B’CB = Π/3 – ∠B’CB =>∠ACB =∠B’CA’ ΔACB is congruent to ΔB’CA’ (SAS) => BA=B’A’ In […]

Gogeometry Problem 242

 dans Euclide Geometry Problem par