From Gogeometry
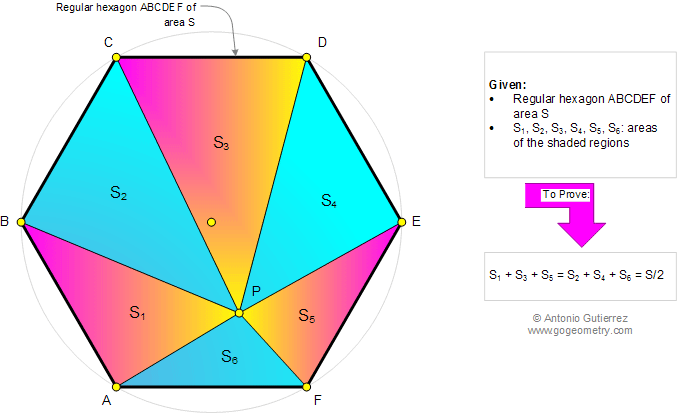

Using

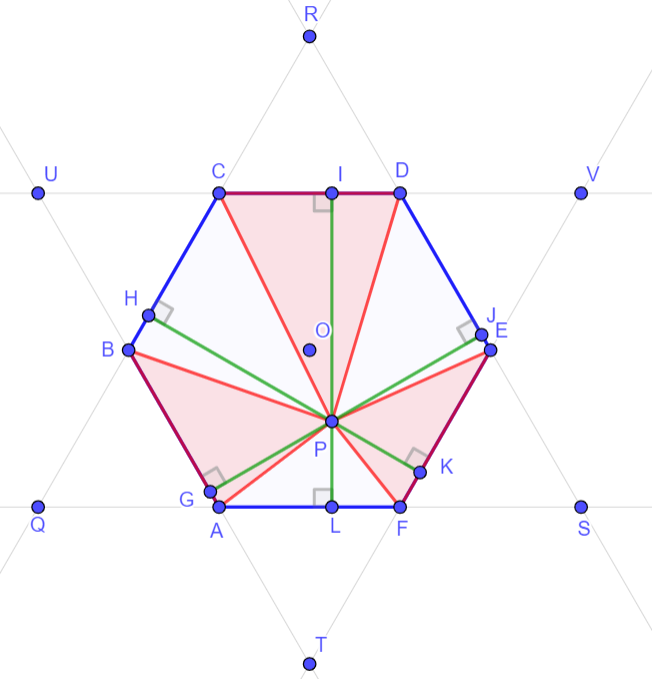
•ABCDEF is a regular hexagon with center O and side c => AB//DE, BC//EF et CD//FA
•Let R=OA=OB=OC=OD=OE=OF
•Define G such as PG⊥ AB. The same for H,I,J,K,L
•AOF is an equilateral triangle with height h, such as BOC, COD, DOE, EOF, FOA
•=> distance between BC and EF =HP+PK=2h such as GJ=HK=IL=2h
•[APB]=c.GP/2 and [DPE]=c.JP/2
•[BPC]=c.HP/2 and [EPF]=c.KP/2
•[CPD]=c.IP/2 and [FPA]=c.LP/2
•Define Q, R and S intersection of BC and AF, BC and DE, DE and AF
•ΔCOD is congruent to ΔCRD, such as ΔAOB with ΔAQB, ΔEOF with ΔESF (AA)
•=> RS=RQ=QS=3c => ΔQRS is equilateral
•From Viviani theorem, PH+PJ+PL=h2 height of ΔQRS =3c.sqrt(3)/2
•In the same way, with ΔTUV : PG+PI+PK=h2
•=> PH+PJ+PL= PG+PI+PK
•=>c(PH+PJ+PL)/2=c(PG+PI+PK)/2
•=>[BPC]+ [DPE]+ [APF] = [APB]+ [CPD]+ [EPF]
•And [ABCDEF]=[BPC]+ [DPE]+ [APF] + [APB]+ [CPD]+ [EPF]