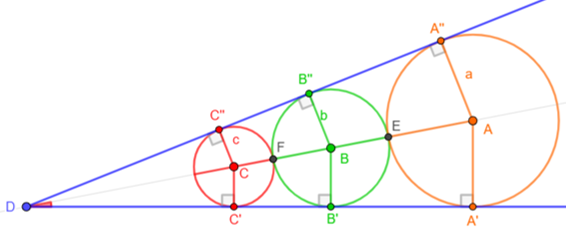
Gogeometry Problem 315 From Gogeometry Using Similar triangles Define n=CDΔBDB’ is similar to ΔCDC’ => BD/BB’=CD/CC’=>(b+c+n)/b=n/c => b+c+n=bn/c => n(b/c-1)=b+c=> (1) n=c(b+c)/(b-c)ΔADA’ is similar to ΔCDC’ => AD/AA’=CD/CC’=>(a+2b+c+n)/a=n/c => ac+2bc+c^2+nc=an => n(a-c)= ac+2bc+c^2=> n= (ac+2bc+c2)/(a-c) => n= c(a+2b+c)/(a-c) (2)(1)&(2) : (b+c)/(b-c)= (a+2b+c)/(a-c)=>(b+c)(a-c)=(a+2b+c)(b-c)=>ab-bc+ac-c^2=ab-ac+2b^2-2bc+bc-c^2=> 2ac=-2c^2=>ac=c^2
