Euclide Geometry Problem

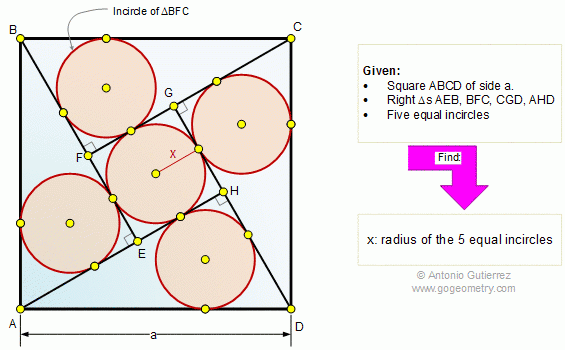
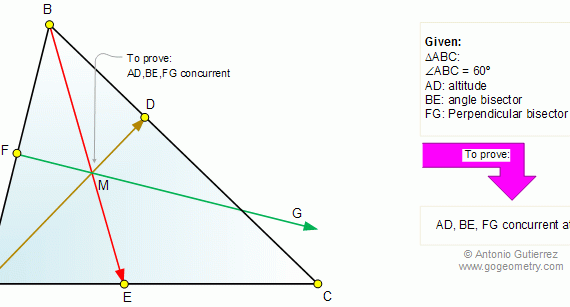
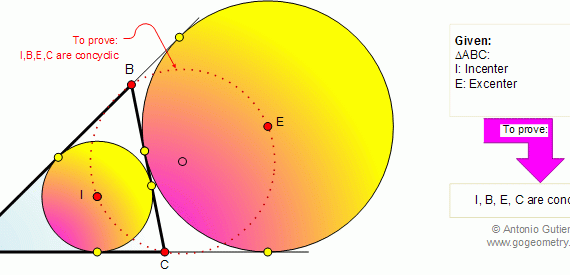
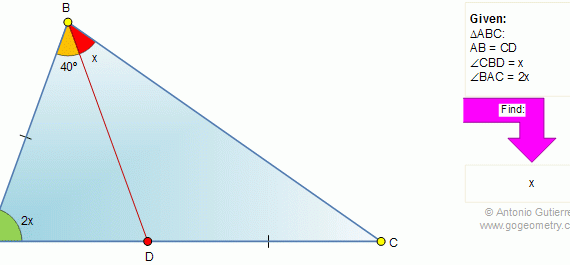
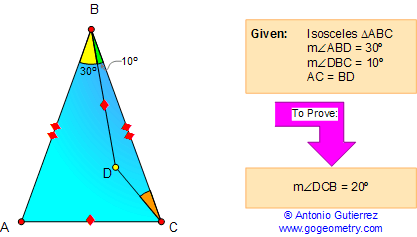
From Gogeometry Using Additional points congruent triangles Equilateral triangle Area of a triangle •ABCDEF is a regular hexagon with center O and side c => AB//DE, BC//EF et CD//FA •Let R=OA=OB=OC=OD=OE=OF •Define G such as PG⊥ AB. The same for H,I,J,K,L •AOF is an equilateral triangle with height h, such […]

Gogeometry Problem 983

 dans Euclide Geometry Problem par
From Gogeometry Using Pythagoras congruent triangles Similar triangles Equilateral triangle Area of a triangle Tangents to a circle Inradius in right triangle •Pythagoras on triangle ΔBFC => (1) BF^2+CF^2=BC^2=a^2 •Incircle in a right triangle => (2) 2x=BF+CF-BC =BF+CF-a •[ABCD]= 4 triangles areas + square with side 2x => (3) S=a^2=2BF.CF+4x^2 […]

Gogeometry Problem 491

 dans Euclide Geometry Problem par
From Gogeometry Using congruent triangles Similar triangles •AD altitude => ∠BDA = π/2 •BE angle bisector =>∠ABE=∠CBE= π/6 •Define M as the intersection of BE and AD •Define F on AB such as BF ⊥ FM •Then we have to demonstrate that FB=FA to prove that FG is perpendicular bisector […]

Gogeometry Problem 663

 dans Euclide Geometry Problem par
From Gogeometry Using central and inscribed angle congruent triangles Concyclic points Tangents to a circle Inscribed angle and tangent to a circle Inradius in right triangle •Point I is on the intersection of the internal angle bisector•=> AI and IB are internal angle bisector •Point O is on the intersection […]

Gogeometry Problem 623

 dans Euclide Geometry Problem par
From Gogeometry Using Area of a triangle Tangents to a circle Inscribed circle of a triangle b=ACAN=AM, AF=AE, MF=NE,CP=CO, CF=CG, PF=OG,BE=BGr=DF=DE=DGx=JM=JN=LO=LPMP=2x S=[ABC]=r(AB+BC+AC)/2 => S=r(AB+CB+b)/2 AB=AE+EB=AF+EBCB=CG+GB=CF+GBAB+CB=AF+CF+EB+GB=b+2BE=> (1) S=r(b+BE) But S=[AMJN]+[MFDENJ]+[PFDGOLP]+[EBGD]S=xAM+(r+x)MF+xCP+(r+x)PF + rEB, knowing that [EBGD]=(rEB+rBG)/2=rEBS=x(AM+MF+CP+PF)+r(MF+PF) + rEB(2) S=xb+2xr + rEB (1) and (2) => S=r(b+BE)=xb+2xr+ rEBbr=xb+ 2xr Therefore x=br/(b+2r)

Gogeometry Problem 418

 dans Euclide Geometry Problem / Géométrie Euclidienne  étiqueté Equal Tangent circles / Incircle / Inradius / radius / Triangle par
From Gogeometry Using Inscribed angles in a circle Equilateral triangle Concyclic points ∠BAD= π/2 => B, A and D are concyclic, circle with center F middle of BD=> FB=FA=FD and ∠BAF=15°In the same way, GC=GA=GE and ∠CAG=15°=>∠FAG=90-15-15=60°ΔFAG is isosceles in A (AF=AG) and ∠FAG=60° => ΔFAG is equilateral Therefore x=FG=BD/2=CE/2=1

Gogeometry Problem 406

 dans Euclide Geometry Problem / Géométrie Euclidienne  étiqueté 15 degrees / Congruence / Midpoints / Right Triangle par
From Gogeometry Using Pythagoras central and inscribed angle Equilateral triangle DC=DA and ∠ADC= π/3 => ΔADC is equilateral∠CAD= π/3, ∠BAC+∠CAD=∠BAD=75° => ∠BAC=15°∠ACD= π/3, ∠BCA+∠ACD=∠BCD=155° => ∠BCA=75°∠BAC=15° et ∠BCA=75° => ∠ABC= π/2 ΔADC is equilateral and EC=ED => ∠AEC= π/2∠ABC= π/2 et ∠AEC= π/2 => A, B, C and E are […]

Gogeometry Problem 405

 dans Euclide Geometry Problem / Géométrie Euclidienne  étiqueté 135 degrees / 60 degrees / 75 degrees / Midpoint / Quadrilateral par