From Gogeomety

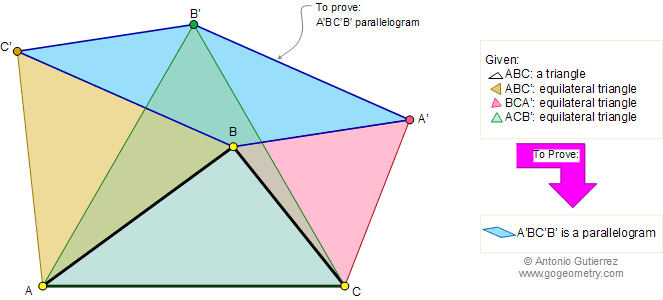
Using :

• Equilateral triangle
• Congruent triangles
• Parallelogram

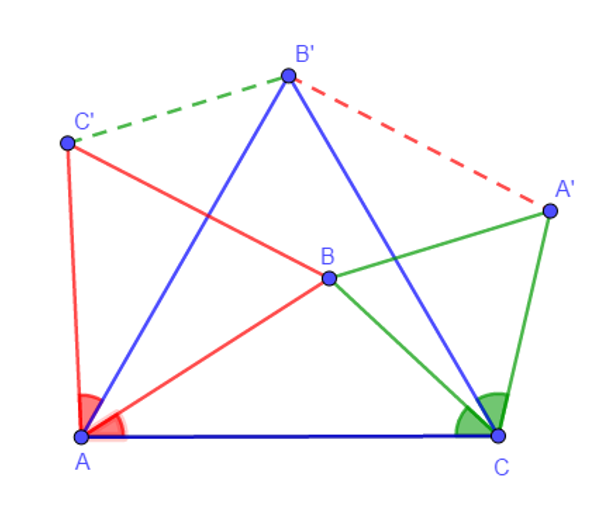
• ΔACB’ and ΔBCA’ are equilateral => ∠ACB’ =∠BCA’ = Π/3
• ∠ACB = ∠ACB’ – ∠B’CB = Π/3 – ∠B’CB
• ∠B’CA’ = ∠BCA’ – ∠B’CB = Π/3 – ∠B’CB
• =>∠ACB =∠B’CA’
• ΔACB is congruent to ΔB’CA’ (SAS) => BA=B’A’
• In the same way:
• ΔCAB’ and ΔBAC’ are equilateral => ∠CAB’ =∠BAC’ = Π/3
• ∠CAB = ∠CAB’ – ∠BAB’ = Π/3 – ∠BAB’
• ∠B’AC’ = ∠BAC’ – ∠BAB’ = Π/3 – ∠BAB’
• =>∠ CAB =∠ B’AC’
• ΔCAB is congruent to ΔB’AC’ (SAS) => BC=B’C’
• BA=B’A’ and BA=BC’ (ΔABC’ equilateral) => B’A’=BC’
• BC=B’C’ and BC=BA’ (ΔBCA’ equilateral) => B’C’=BA’
• => B’A’=BC’ and B’C’=BA’ => B’A’BC’ is a parallelogram