Enigma

Enigmes & Problèmes scientifiques

Euclide Geometry Principles

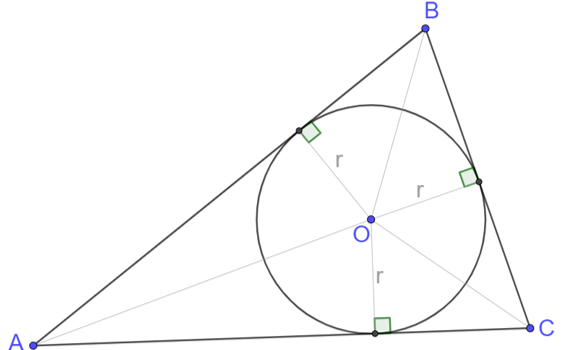
ΔABC right triangle in C Define r its inradius, a=BC,b=AC and c=A PCRO is square => PC=CR=r AC et AB tangents to the circle=>AP=AQ, BQ=BR and CP=CR b=AC=AP+PC, a=BC=BR+RC AC+BC=b+a=AP+r+BR+r=2r+AP+BR AP=AQ, BR=BQ => AC+BC=b+a=2r+AQ+BQ=2r+AB=2r+c a+b=2r+c Therefore r=(a+b-c)/2 Define p as the semi-perimeter of the triangle, p=(a+b+c)/2 Therefore r =p-c

Inradius in right triangle

dans Euclide Geometry Principles par Harvey Littleman

define a CB, b=AC and c=AB Define S as the area of the triangle S=r.a/2 + r.b/2 + r.c/2 Therefore S=r(a+b+c)/2 and r=2S/(a+b+c)

Inscribed circle of a triangle

dans Euclide Geometry Principles par Harvey Littleman

CircleO1 intersects CircleO2 in A and B By symmetry, CA=CB O2A=O2B => Δ AO2B is isosceles in O2 =>AC ⊥ CO2 In the same way with CircleO1: O1O2⊥ AB

Intersection of two circles

dans Euclide Geometry Principles par Harvey Littleman

Define h=HB Case 1) H in AC a^2=h^2+(b-m)^2 c^2=h^2+m^2 a^2-c^2=b^2-2mb Therefore a^2=b^2+c^2-2mb Case 2) A in HC a^2=h^2+(b+m)^2 c^2=h^2+m^2 a^2-c^2=b^2+2mb Therefore a^2=b^2+c^2+2mb

Proposition 13 Euclide Book II (Law of Cosines)

dans Euclide Geometry Principles par Harvey Littleman

AD tangent to circle with center O C on this circle => ∠BAD= ∠BCA Demonstration Define E in the circle such as E, O and A are colinear ∠0AD=90° and ∠ECA= 90° ∠BAE intercepts arc BE and ∠BCE intercepts arc BE => ∠BAE= ∠BCE ∠0AD= ∠0AB+∠BAD=90° ∠ECA= ∠ECB+∠BCA=90° […]

Inscribed angle and tangent to a circle

dans Euclide Geometry Principles par Harvey Littleman

AG and AH are tangent to a circle with center O =>AG=AH Proof AG and AH are tangent to a circle with center O <=>∠AHO=∠AGO= π/2 OH=OG=r => O is at the same distance of AH and AG => O in on the angle bissector of ΔGAH => ∠GAO=∠HAO =>ΔOAG […]

Tangents to a circle

dans Euclide Geometry Principles par Harvey Littleman

Points A, B, C and D on a circle <=> ∠ACB= ∠ADB

Concyclic points

dans Euclide Geometry Principles par Harvey Littleman

From Gogeometry Using : Isometric transformation Additional points congruent triangles Area of a triangle Define a square ABCD Define E in AB, AE=a and EB=b Define F in BC such as BF=b and FC=a [ABCD]=[HIGD]+[EBFI]+[AEIH]+[FCGI] [AEIH]=[FCGI]=ab=>[ABCD]=a^2+b^2+2ab=(a+b)^2 Cut [AEIH] in 2 triangles T1=AEI and T2=AHI Cut [FCGI] in 2 triangles T3=FCG […]

Pythagoras theorem

dans Euclide Geometry Principles / Euclide Geometry Problem par Harvey Littleman

Points A, B and C on a circle with the incenter O <=> ∠AOB =2 ∠ACB

Central and inscribed angle

dans Euclide Geometry Principles par Harvey Littleman

Points A, B, C and D on a circle <=>∠ACB= ∠ADB

Inscribed angles in a circle

dans Euclide Geometry Principles par Harvey Littleman