From Gogeometry
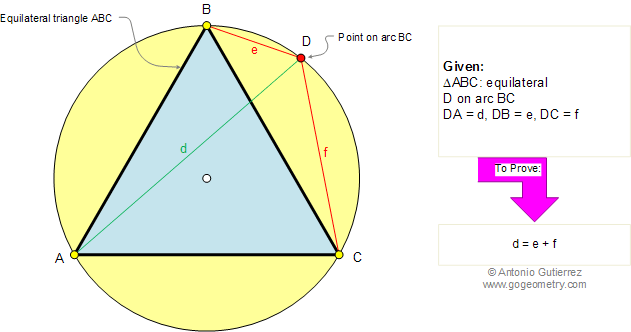
 Using :
Using :
Additional points
Inscribed angles in a circle
congruent triangles
Equilateral triangle

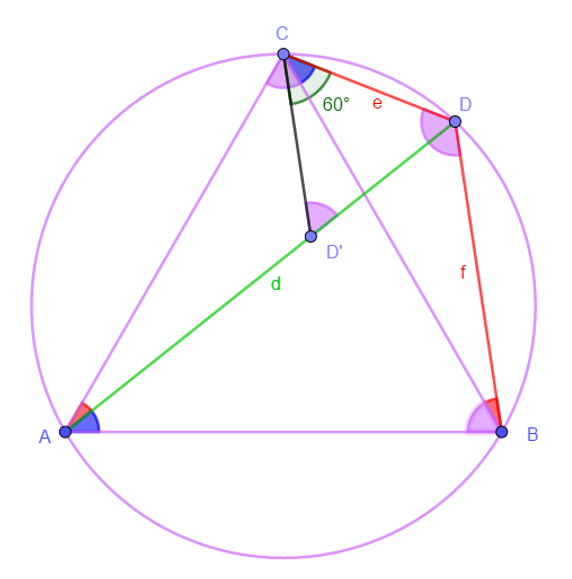
- CAD intercepts arc CD such as CBD => ∠CAD= ∠CBD
- Define D’ n AD such as AD’C is congruent to BDC
- => AD’=f and ∠ACD’= ∠BCD
- ∠ACD= ∠ACB+ ∠BCD=Π/3+ ∠BCD
- And ∠ACD= ∠ACD’+ ∠D’CD=∠BCD+ ∠D’CD => ∠D’CD = Π/3
- CDA intercepts arc CA such as ABC => ∠CDA= ∠ABC=Π/3
- ∠D’CD = Π/3 and ∠CDA= ∠CDD’= Π/3 => ΔD’CD is equilateral
- =>D’D=CD=e
- d=AD=AD’+D’D therefore d=e+f