Euclide Geometry Problem

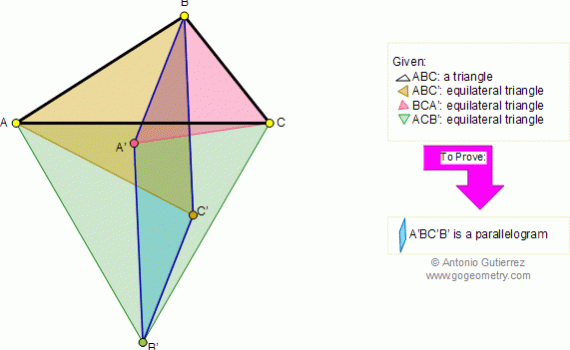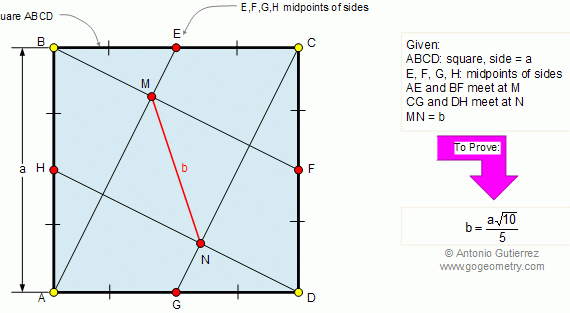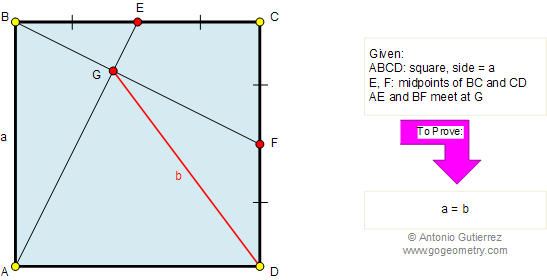
From Gogeometry : Using : Congruent triangles ΔABE is congruent to ΔBCF by rotation of pi/2 => <AGF=90° Define H as the middle of AB and K as the middle of AG By construction HD//BF AH=HB=>AK=KG <AGF=90° => <AKD=90° ΔDKG is congruent to ΔDKA (SAS) =>DG=DA Therefore a=b

Gogeometry Problem 238

 dans Euclide Geometry Problem par
From Gogeometry : Using : Equilateral triangle Congruent triangles Parallelogram   ΔCAB’ and ΔC’AB are equilateral => ∠CAB’=∠C’AB=Π/3 ∠BAB’=a+∠CAB’=∠BAC’+a’ => a=a’ AC’=AB and AB’=AC and a=a’=> ΔBAC and ΔB’AC’ are congruent (SAS) =>B’C’=BC But BC=BA’=>B’C’=BA’ In the same way : ∠BCA’=∠B’CA=Π/3 ∠BCA=c= Π/3 – ∠ACA’ ∠B’CA’=c’= Π/3 – ∠ACA’ =>c=c’ […]

Gogeometry Problem 240

 dans Euclide Geometry Problem par
From Gogeometry :   Using : Area of a triangle Pythagoras Define O intersection of AE and HD and P intersection of BF and GC ABE is congruent to CBF by rotation of pi/2 => <DNP=<FPC=<NOM=<PME=90° Define x=OA and y=OH Define S1=[AOH]= x y /2 [AOH]= [HOB]= [BME]= [EMC]= [CPF]= […]

Gogeometry Problem 239

 dans Euclide Geometry Problem par