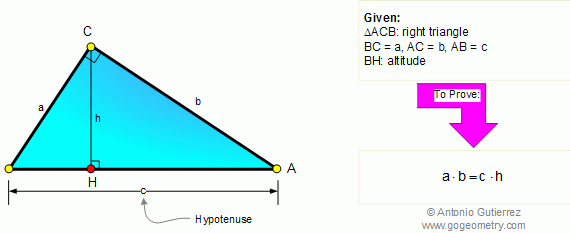
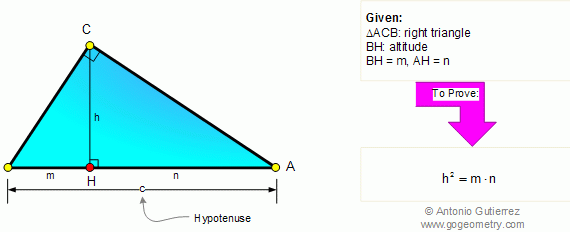
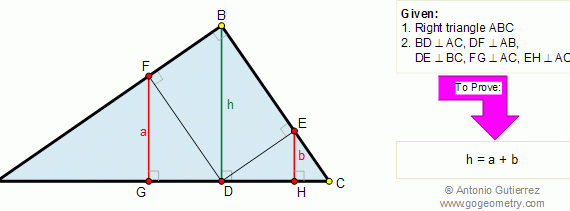
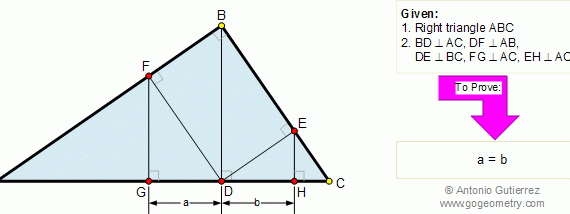
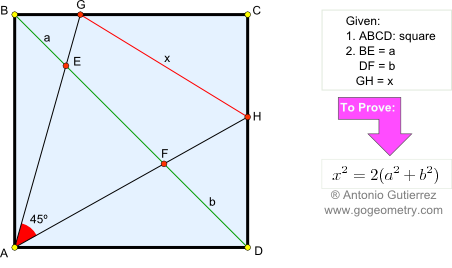
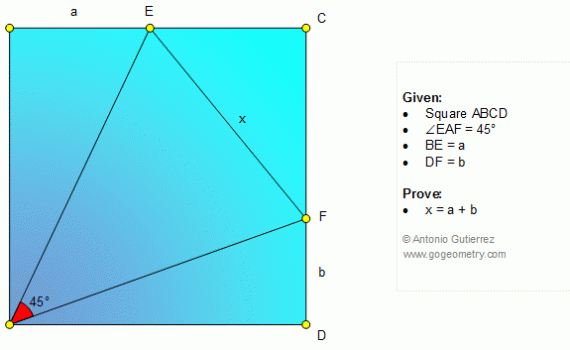
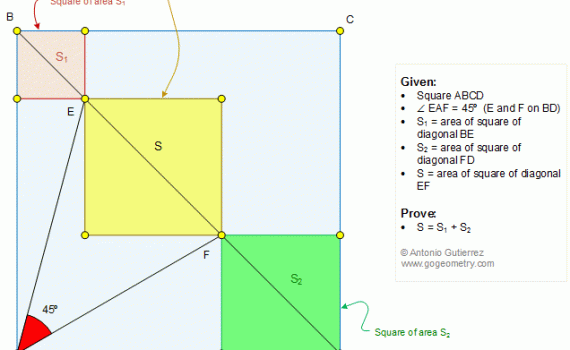
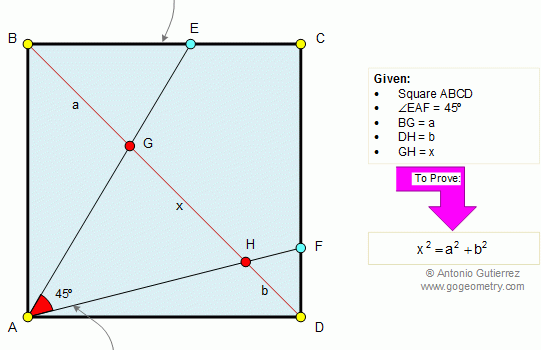
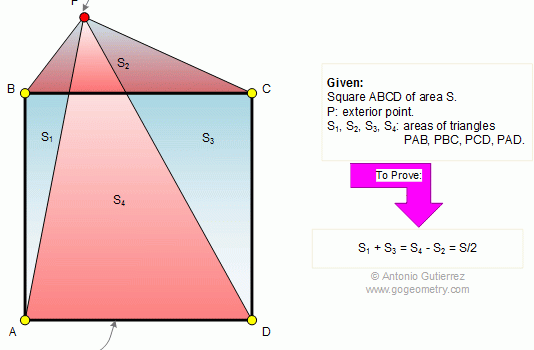
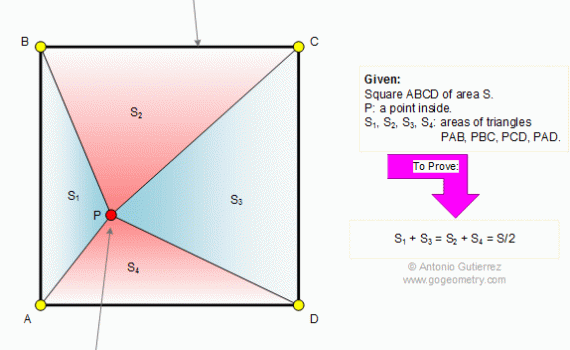
From Gogeometry Using : Pythagoras Area of a triangle S=[ABC] S=a.b/2 But also S=c.h/2 Therefore a.b=c.h
Euclide Geometry Problem
From Gogeometry Using : Pythagoras (1) ΔABC : AC^2+BC^2=c^2 (2) ΔAHC : AC^2 =h^2+n^2 (3) ΔBHC : BC^2=h^2+m^2 c=m+n, c^2=(m+n)^2=m^2+n^2+2mn (1,2,3) h^2+n^2+h^2+m^2=m^2+n^2+2mn 2h^2=2mn Therefore h^2=m.n
Gogeometry Problem 266
From Gogeometry Using : Additional points congruent triangles Solution of a previous problem 218 DB=GF+FJ From problem 217, ΔJBF is congruent to ΔHDE (AAA) => JF=EH Therefore a+b=h
Gogeometry Problem 218
From Gogeometry Using : Isometric transformation Additional points congruent triangles Define J in FG such as JG ⊥ JB => JB=GD ED//BF => ∠JBF=∠HDE In ΔHDE, ∠HDE + ∠DEH =90° => in ΔJBF, ∠JBF + ∠BFJ =90° =>∠JFB = ∠HED FB=DE => ΔJBF is congruent to ΔHDE (AAA) => JB=HD […]
Gogeometry Problem 217
From Gogeometry Using : Pythagoras Inscribed angles in a circle central and inscribed angle Concyclic points Solution of a previous problem : Pb367 AD⊥AH => A, D, H are concyclic Arc EH : ∠EDH=45° and ∠EAH=45° => A, D, H and E are concyclic Arc AE : ∠EDA=45° => ∠EHA=45° […]
Gogeometry Problem 188
From Gogeometry Using : Isometric transformation Additional points congruent triangles Define α = ∠BAF and β = ∠DAE α+β+45°=90° => α+β = 45° Define E’ rotation of E anticlockwise with an angle of 90° =>AE=AE’, β = ∠DAE = ∠BAE’ ∠FAE’= α+β = 45° ΔFAE’ is congruent to ΔFAE (SAS) […]
Gogeometry Problem 1076
From Gogeometry Using : Pythagoras Define a,b and x respectively hypothenuse of S1, S2 and S S1 is a square => S1= a^2/2 In the same way, S2= b^2/2 and S= x^2/2 From Pb 367 we know that x^2=a^2+b^2 => (x^2)/2=(a^2)/2+(b^2)/2 Therefore S=S1+S2
Gogeometry Problem 1338
From Gogeometry Using : Isometric transformation Additional points Pythagoras congruent triangles Define H’ rotation of H with angle –90° and center A =>AH=AH’ and BH’=DH=b => BH’ ⊥DH <=> BH’ ⊥BG ∠HAG=45° and ∠HAH’=90° => ∠GAH’=45° ΔGAH is congruent to ΔGAH’ (SAS) => GH’=GH=x BH’=b, BG=a, BH’ ⊥BG and GH’=x […]
Gogeometry Problem 367
From Gogeometry Using : Additional points Area of a triangle Define a = side of square ABCD Define h1,h2,h3 and h4 the heights respectively of S1, S2, S3 and S4 h1+h3=a, h4-h2=a S=[ABCD]=a^2 2S1=a.h1, 2S3=a.h3 2S1+2S3=a(h1+h3)=a^2 2S2=a.h2, 2S4=a.h4 2S4-2S2=a(h4-h2)=a^2 Therefore <b>S1+S3=S4-S2=S/2</b>
Gogeometry Problem 357
From Gogeometry Using : Area of a triangle Define h1,h2,h3 and h4 the heights respectively of S1, S2, S3 and S4 Define a the side of the square ABCD S1=a.h1/2 S2=a.h2/2 S3=a.h3/2 S4=a.h4/2 And h1+h3=h2+h4=a S1+S3=a(h1+h3)/2=a^2/2 S2+S4=a(h2+h4)/2=a^2/2 S=[ABCD]=a^2 Therefore S1+S3= S2+S4=S/2