From Gogeometry
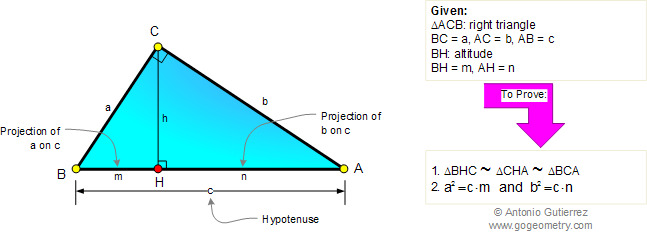

Using :

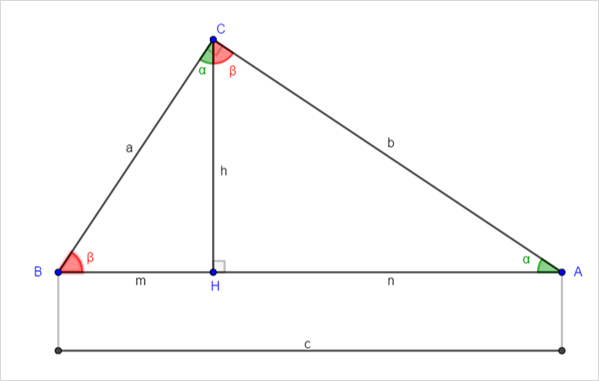
- In ΔBHC : ∠ABC + ∠HCB =90°
- In ΔBCA : ∠HCA + ∠HCB =90° => ∠HCA = ∠ABC=β
- In ΔCHA : ∠HCA +∠BAC=90° => ∠HCB =∠BAC= α
- => ΔBHC is similar to ΔCHA (aaa=β90α)
- and ΔBHC is similar to ΔBCA (aaa=β90α)
- Therefore ΔBHC, ΔCHA and ΔBCA are similar
- c=m+n
- (1) In ΔBHC : a^2 = m^2+h^2
- (2) In ΔCHA : b^2 = h^2+n^2
- (3) In ΔBCA : a^2+b^2 = (m+n)^2
- (4=1+2) a^2+b^2 = m^2+n^2+2h^2
- (5=4+3) m^2+n^2+2h^2 = (m+n)^2 = m^2+n^2+2mn => h^2= mn
- (1+5): a^2 = m^2+h^2=m^2+mn =m(m+n)=> a^2=cm
- (2+5): b^2 = n^2+h^2=n^2+mn=n(m+n)=> b^2=cn