Gogeometry Problem 1

 dans Euclide Geometry Problem par Harvey Littleman

---

From Gogeometry

 

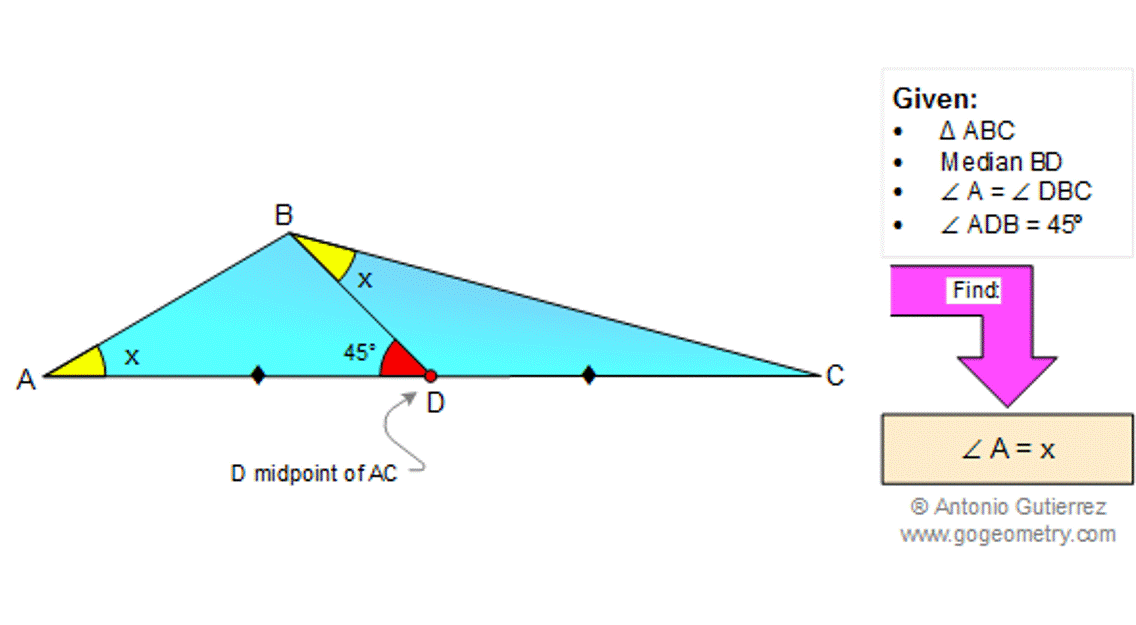
Using :

• Isometric transformation
• Additional points
• Pythagoras
• congruent triangles
• Equilateral triangle

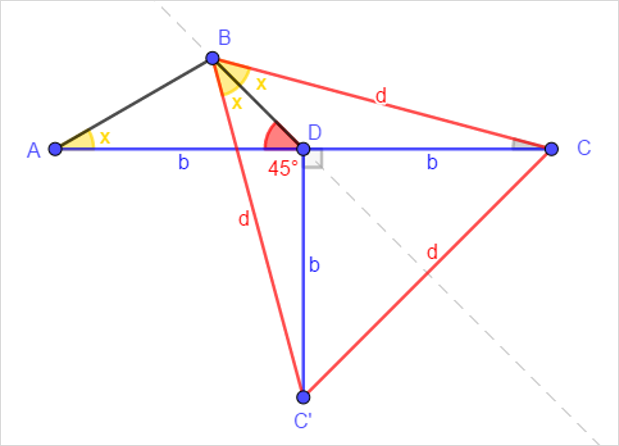
• Let b=AD=DC and d=BC
• ∠BAC= ∠CBD and ∠BCD= ∠BCA
• => ΔCAB is similar to ΔCBD
• =>AC/BC=CB/CD=AB/BD => 2b^2=d^2, which means that d is the hypothenuse of a right triangle with side b
• Define C’ such as ΔDBC’ is the symmetry of ΔDBC by BD
• => ΔDBC’ is congruent to ΔDBC
• ∠BDC=180°-45°=135° = ∠BDC’ => ∠CDC’=360-135-135=90°
• => CC’=d and ΔCBC’ is equilateral
• ∠DBC= ∠DBC’= 2x=60°
• Therefore x=30°

---

---