From Gogeometry

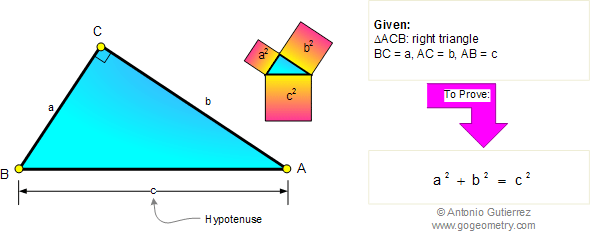
Using :

• Isometric transformation
• Additional points
• congruent triangles
• Area of a triangle

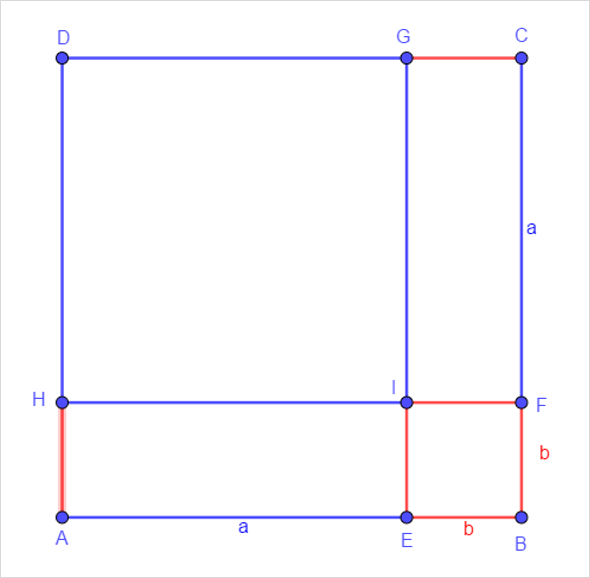
• Define a square ABCD
• Define E in AB, AE=a and EB=b
• Define F in BC such as BF=b and FC=a
• [ABCD]=[HIGD]+[EBFI]+[AEIH]+[FCGI]
• [AEIH]=[FCGI]=ab=>[ABCD]=a^2+b^2+2ab=(a+b)^2

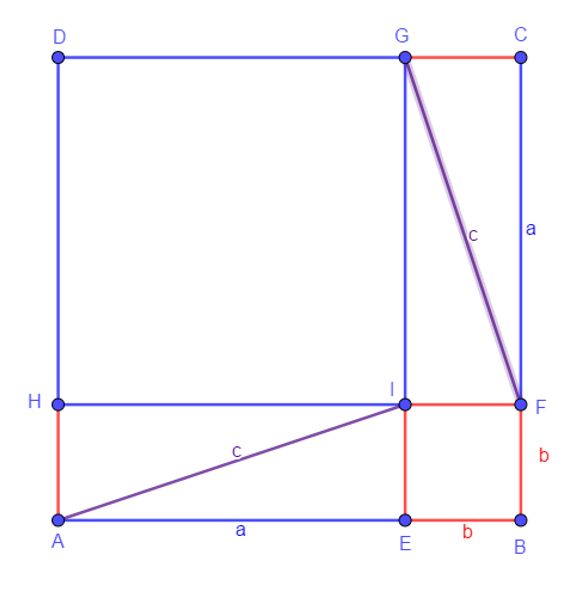
• Cut [AEIH] in 2 triangles T1=AEI and T2=AHI
• Cut [FCGI] in 2 triangles T3=FCG and T4=FIG
• AEI, AHI, FCG and FIG are congruent with surface T=ab/2
• Define c=AI=FG

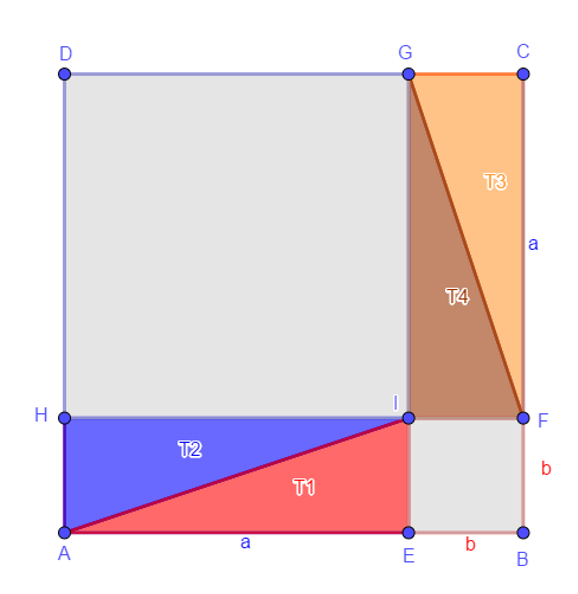
• [ABCD]=a^2+b^2+4T

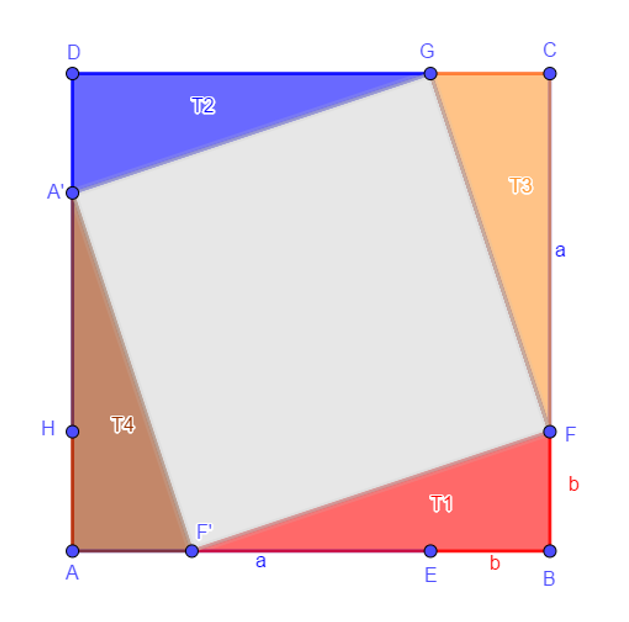
• Translate T2 such as HI becomes DG
• Translate T1 such as EI becomes BF
• Translate T4 such AS GI becomes A’A
• By symetry, A’F’FG is a square => [A’F’FG]=c^2
• [ABCD] =4T+[A’F’FG] =4T+c^2
• But [ABCD]=a^2+b^2+4T
• Therefore a^2+b^2=c^2