Enigma

Enigmes & Problèmes scientifiques

Euclide Geometry Problem

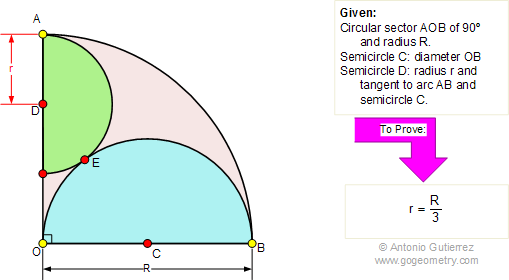
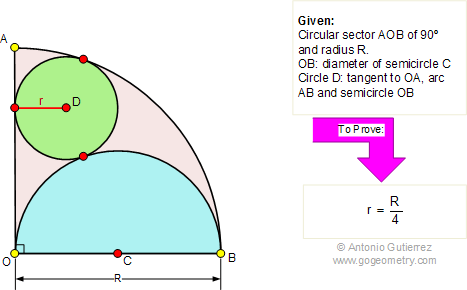
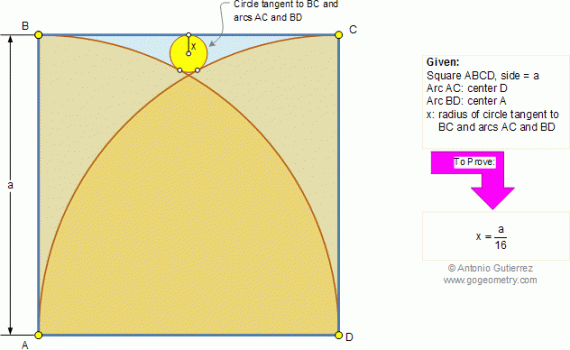
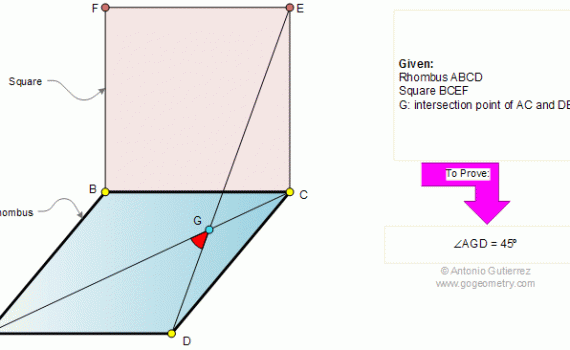
From Gogeometry Define a=AB=BC=AC DC and DB tangents to Circle O1 => DG=DE=bAD and AB tangents to Circle O1 => AG=AJ=dDB and BA tangents to Circle O1 => BE=BJ=c DB and BC tangents to Circle O2 => BF=BK=eDC and BC tangents to Circle O2 => CI=CK=f a=d+c=e+fDF=b+c+e, DI=b+d+a+fDC and DB […]

Gogeometry Problem 1372

dans Euclide Geometry Problem étiqueté Altitude / Equilateral Triangle / Exradius / Exterior Cevian / Inradius par Harvey Littleman

From Gogeometry Using : Additional points Similar triangles Equilateral triangle Define 0 middle of BC. O is the center of semicircle OD diameter BC Define a=OB=OD=OC => AB=AC=BC=2a Arc BD=arc DE=arc EC => ∠BOD=∠DOE=∠EOC=Π/3 OB=OD=a and ∠BOD=Π/3 =>BD=a, ΔBOD is equilateral and BD//AC In the same way, DE=a, ΔDOE […]

Gogeometry Problem 326

dans Euclide Geometry Problem étiqueté Equal arcs par Harvey Littleman

From Gogeometry Using : Pythagoras Proposition 13 Euclide Book II In ΔDMF : DM^2=DF^2+FM^2 (1) DM^2= (r-x/2)^2+x^2 In ΔAMD : AM^2=AD^2+DM^2 -2xAD (Proposition 13 Euclide Book II) r^2= r^2+ DM^2 -2xr (2) DM^2=2xr (1) and (2) 2xr=(r-x/2)^2+x^2 2xr=r^2-xr+x^2/4+x^2 3xr=r^2+5x^2/4 Dividing by x^2 (x not equal to 0) =>3r/x=5/4+(r/x)^2 Let y=r/x […]

Gogeometry Problem 336

dans Euclide Geometry Problem étiqueté a Common Tangent and a Square / Two equal circles par Harvey Littleman

From Gogeometry Using : Isometric transformation Additional points Pythagoras Similar triangles Tangents to a circle Define O middle of AB, r=ED AD^2+AO^2=DO^2 a^2+(a/2)^2=(a/2+r)^2 a^2+a^2/4=a^2/4+r^2+ar r^2+ar-a^2=0 ∆=a^2+4a^2=5a^2 r>0 => r=(a.sqr(5)-a )/2 Draw a square symetryc of ABCD by O =>D becomes D’, C becomes C’, E becomes E’ => C’D’BA is […]

Gogeometry Problem 458

dans Euclide Geometry Problem étiqueté Circular Sector / Internal Common Tangent / Measurement / Semicircle / square par Harvey Littleman

From Gogeometry Using : Additional points Pythagoras Solution of a previous problem Tangents to a circle Proposition 13 Euclide Book II R radius of CircleO, and r of CircleF Define ro radius of CircleO , rd of CircleD, rc of CircleC and rf of CircleF Define G intersection of OA […]

Gogeometry Problem 285

dans Euclide Geometry Problem par Harvey Littleman

From Gogeometry Using : Pythagoras Define h=OF OA=OB=R D, E and C are aligned ΔCOD is right in O => DC^2=OC^2+OD^2 OD=r+h => (1) : (r+R/2)^2=(R/2)^2+(r+h)^2 => (1) : (r+R)^2=R^2+4(r+h)^2 OB=OA => R=2r+h => r+h=R-r (1) : (r+R)^2=R^2+4(R-r)^2 => r^2+2rR+R^2=R^2+4(R^2-2rR+r^2) => 6rR= 3r^2 Therefore 3R=r

Gogeometry Problem 284

dans Euclide Geometry Problem par Harvey Littleman

From Gogeometry Using : Additional points Inscribed angles in a circle central and inscribed angle Tangents to a circle Inscribed angle and tangent to a circle Without using : Law of cosines Define : F the tangent intersection of CirleD and CircleO E intersection of CircleD and OA G intersection […]

Gogeometry Problem 283

dans Euclide Geometry Problem par Harvey Littleman

From Gogeometry Using : Inscribed angles in a circle central and inscribed angle congruent triangles Similar triangles Tangents to a circle Inscribed angle and tangent to a circle Without using : Pythagoras Define G the center of CircleG with radius x Define the point E as the only point […]

Gogeometry Problem 276

dans Euclide Geometry Problem par Harvey Littleman

From Gogeometry Using : Inscribed angles in a circle congruent triangles Concyclic points ABCD is a rhombus => ΔACD is congruent to ΔACB => ∠ACD = ∠ACB => ΔGCD is congruent to ΔGCB (SAS) => ∠GDC = ∠GBC ABCD is a rhombus =>CE=CD => ΔDCE is isosceles in C => […]

Gogeometry Problem 354

dans Euclide Geometry Problem par Harvey Littleman

From Gogeometry Using : Pythagoras Area of a triangle Define c=AB S=[ABC]=a.b/2=c.h/2 => a.b=c.h c=a.b/h => c^2=a^2.b^2/h^2 Pythagoras => a^2+b^2=c^2 => a^2+b^2=a^2.b^2/h^2 dividing by a^2.b^2 => 1/b^2 + 1/a^2 = 1/h^2

Gogeometry Problem 268

dans Euclide Geometry Problem par Harvey Littleman