Gogeometry Problem 354

 dans Euclide Geometry Problem par Harvey Littleman

---

From Gogeometry

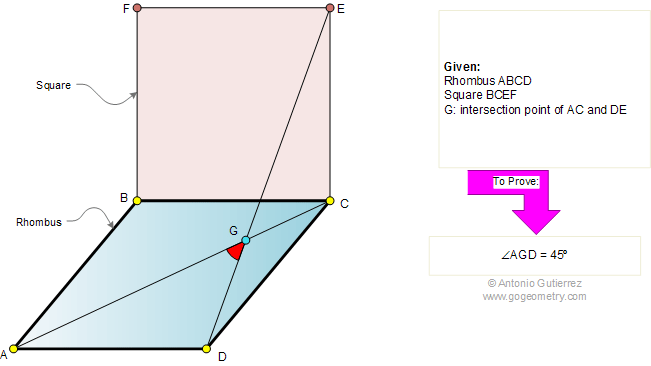
Using :

• Inscribed angles in a circle
• congruent triangles
• Concyclic points

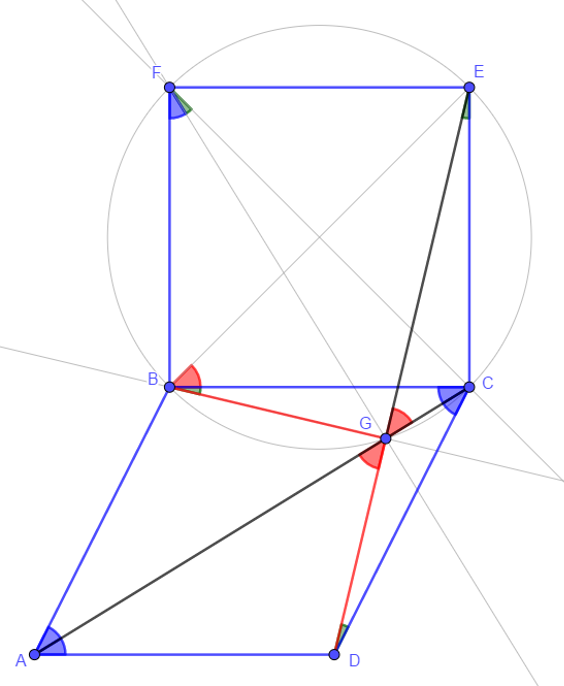
• ABCD is a rhombus => ΔACD is congruent to ΔACB
• => ∠ACD = ∠ACB
• => ΔGCD is congruent to ΔGCB (SAS)
• => ∠GDC = ∠GBC
• ABCD is a rhombus =>CE=CD => ΔDCE is isosceles in C
• => ∠GEC = ∠GDC
• ∠GEC = ∠GBC => B, G, C, E are concyclic

• ∠AGD = ∠EGC
• Arc CE : ∠EBC = ∠EGC
• ∠EBC = 45° therefore ∠EGC = 45°

---

---