From Gogeometry

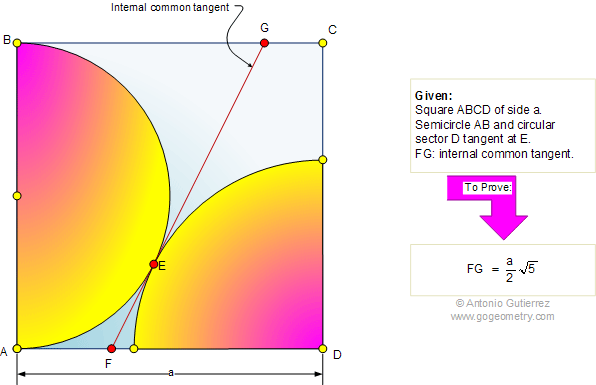
Using :

• Isometric transformation
• Additional points
• Pythagoras
• Similar triangles
• Tangents to a circle

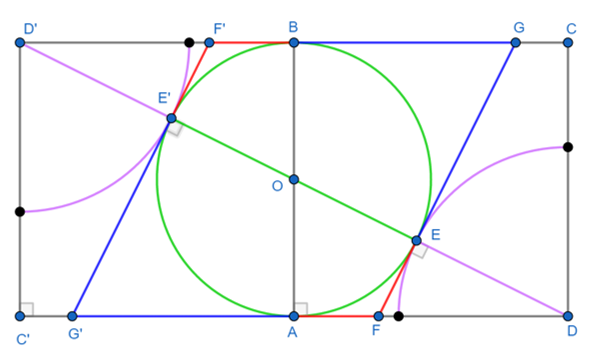
• Define O middle of AB, r=ED
• AD^2+AO^2=DO^2
• a^2+(a/2)^2=(a/2+r)^2
• a^2+a^2/4=a^2/4+r^2+ar
• r^2+ar-a^2=0
• ∆=a^2+4a^2=5a^2
• r>0 => r=(a.sqr(5)-a )/2
• Draw a square symetryc of ABCD by O
• =>D becomes D’, C becomes C’, E becomes E’
• => C’D’BA is a square, D, E, O, E’, D’ are colinear
• => EG=E’G’ and FE=F’E’
• FG ꓕ DD’ => F’G’ ꓕ DD’
• ∆ADO is similar to ∆E’DG’ and EDF (aa)
• =>AD/AO=2=E’D/E’G’=ED/EF
• E’D=a+r = 2 EG and ED=r=2 EF
• =>EF+EG=(r+a+r)/2=r+a/2=(a.sqr(5)-a )/2+a/2= a.sqr(5)/2
• Therefore FG= a.sqr(5)/2