From Gogeometry
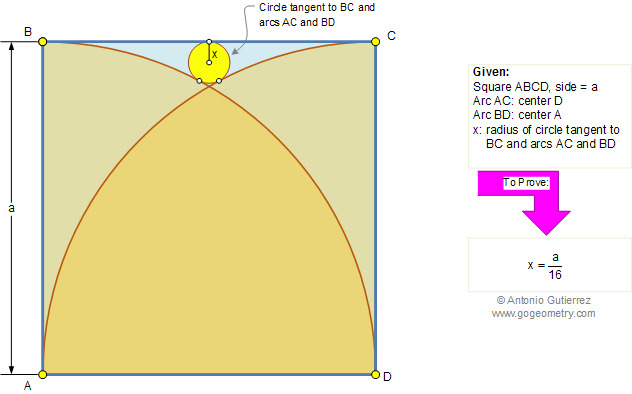

Using :
- Inscribed angles in a circle
- central and inscribed angle
- congruent triangles
- Similar triangles
- Tangents to a circle
- Inscribed angle and tangent to a circle
Without using :

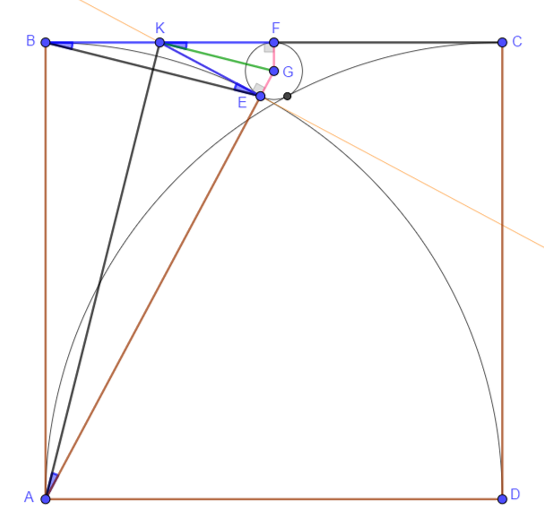
- Define G the center of CircleG with radius x
- Define the point E as the only point of intersection between CircleG and CircleA => A, E and G are aligned
- Define K in BC such as KE is tangent to CircleA
- BC is tangent of circleA on B =>CBE intercepts arc BE of circleA =>2 ∠CBE= ∠BAE
- EK is tangent of circleA on E =>KEB intercepts arc BE of circleA
- => ∠KEB= ∠KBE => BKE is isosceles in K => KB=KE and ∠CKE= 2 ∠KBE
- Define F on BC such as F belongs to CircleG => GF⊥BC
- => KB=KE and KE⊥GE and KF⊥FG and GF=GE=x
- KF is tangent to CircleG and KE is tangent to CircleG => KE=KF
- => ΔKFG is congruent to ΔKEG (SAS)
- => ∠FKG= ∠EKG => ∠FKE= 2 ∠FKG => ∠FKG= ∠KBE
- ΔAEK is congruent to ΔABK (SAS) => ∠ABK= ∠FKG
- =>ΔABK is similar to KFG => AB/BK=KF/FG
- By symmetry F is in the middle of BC, BK=KF => BK=AB/4=a/4
- AB/BK=4=KF/FG =>KF=4FG, KF=AB/4=>KF=AB/16
- Therefore x=a/16