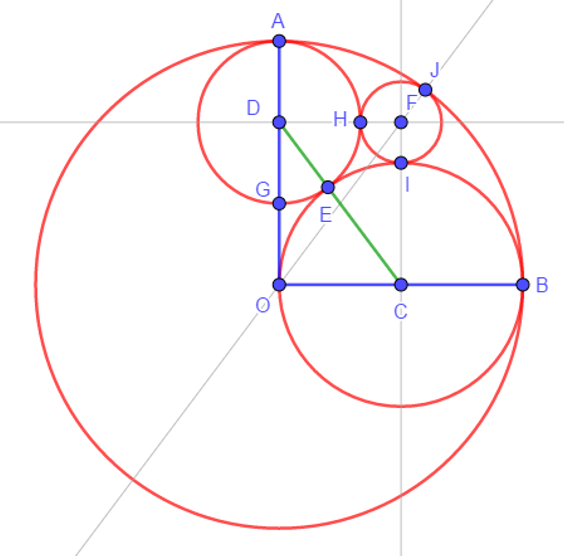
From Gogeometry


Using :
- Additional points
- Pythagoras
- Solution of a previous problem
- Tangents to a circle
- Proposition 13 Euclide Book II

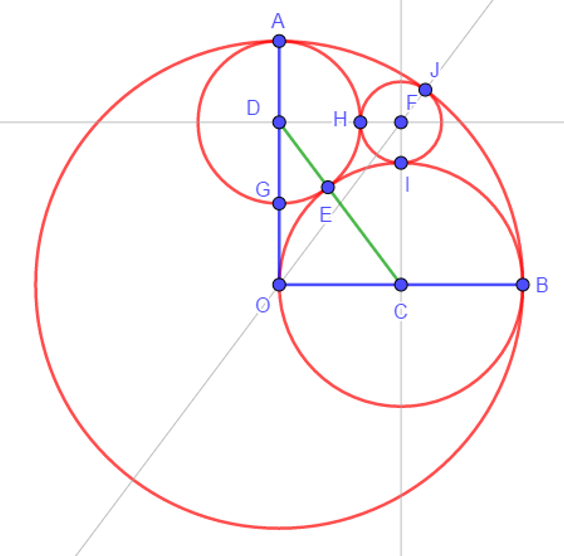
- R radius of CircleO, and r of CircleF
- Define
- ro radius of CircleO , rd of CircleD, rc of CircleC and rf of CircleF
- Define
- G intersection of OA and CircleD
- H intersection of CircleD and CircleF
- I intersection of CircleC and CircleF
- J intersection of CircleO and CircleF
- CircleD if tangent to CircleF => D, H and F are aligned and DF=rd+r
- CircleC if tangent to CircleF => C, I and F are aligned and CF=rc+r
- CircleO if tangent to CircleF => O, F and J are aligned and OF=ro-r

- Let’s say R=6 regardless of the units
- OB=6
- OC=3
- From Pb 284:
- AD=2
- Therefore
- OD=4
- OF=6-r
- DF=2+r
- CF=3+r
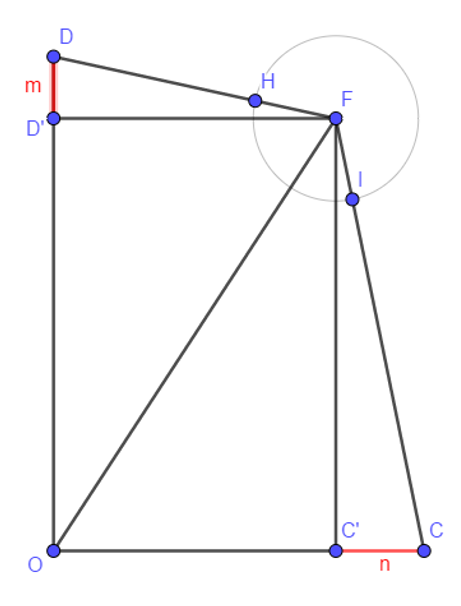
- Is ODFC a rectangle?
- If it is true, then, obviously (DF=OC) and therefore r=1
- Let’s suppose ODFC is not a rectangle…
- Define D’ and C’ respectively orthogonal projection of D and C on OA and OB
- Define m=DD’ and n=CC’
- We have 4 different cases
CASE A : D’ and C’ are respectively in OD and OC

Proposition 13 Euclide Book II => OF^2=OD^2+DF^2-2 OD DD’
- (6-r)^2=(4)^2+(2+r)^2-2(4)m
- 36-12r+r^2=16+4+4r+r^2-8m
- 16+8m=16r
- 2+m=2r
- m=2r-2
Proposition 13 Euclide Book II => OF^2=OC^2+CF^2-2 OC CC’
- (6-r)^2=(3)^2+(3+r)^2-2(3)n
- 36-12r+r^2=9+9+6r+r^2-6n
- 18+6n=18r
- 3+n=3r
- n=3r-3
- OD’FC’ is a rectangle=>
- OC’^2+OD’^2=OF^2
- (3-n)^2+(4-m)^2=(6-r)^2
- (3- 3r+3)^2+(4- 2r+2)^2=(6-r)^2
- (6-3r)^2+(6-2r)^2=(6-r)^2
- 36-36r+9r^2+36-24r+4r^2=36-12r+r^2
- 12r^2-48r+36=0
- r^2-4r+3=0
- Delta=16-4×3=4
- r=(4+-2)/2
- r=3 or r=1
- If r=3 => m=4 flat triangle : impossible
- Therefore r=1 => m=0 and n=0
- Therefore ODFC is a rectangle
CASE B : D’ in OD and C in OC’
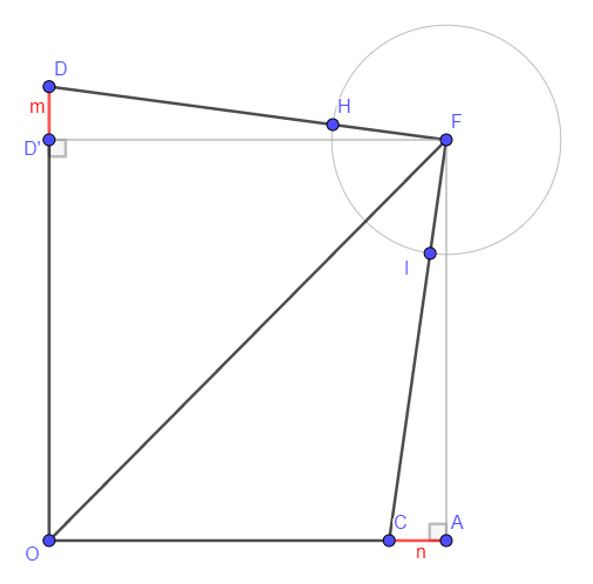
- Proposition 13 Euclide Book II => OF^2=OC^2+CF^2-2 OC CC’
- (6-r)^2=(3)^2+(3+r)^2-2(3)n
- 36-12r+r^2=9+9+6r+r^2-6n
- 18+6n=18r
- 3+n=3r
- n=3r-3
- Proposition 13 Euclide Book II => OF^2=OC^2+CF^2+2 OC CC’
- (6-r)^2=(3)^2+(3+r)^2+2(3)n
- 36-12r+r^2=9+9+6r+r^2+6n
- 18-6n=18r
- 3-n=3r
- n=3-3r
- OD’FC’ is a rectangle=>
- OC’^2+OD’^2=OF^2
- (3-n)^2+(4-m)^2=(6-r)^2
- (3- 3r+3)^2+(4- 2r+2)^2=(6-r)^2
- (6-3r)^2+(6-2r)^2=(6-r)^2
- 36-36r+9r^2+36-24r+4r^2=36-12r+r^2
- 12r^2-48r+36=0
- r^2-4r+3=0
- Delta=16-4×3=4
- r=(4+-2)/2
- r=3 or r=1
- If r=3 => m=4 flat triangle
- Therefore r=1 => m=0 and n=0
- Therefore ODFC is a rectangle
CASE C : D in OD’ and C’ in OC
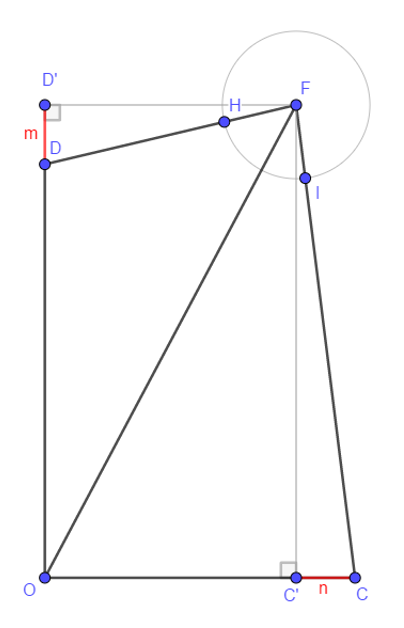
- Proposition 13 Euclide Book II => OF^2=OD^2+DF^2+2 OD DD’
- (6-r)^2=(4)^2+(2+r)^2+2(4)m
- 36-12r+r^2=16+4+4r+r^2+8m
- 16-8m=16r
- 2-m=2r
- m=2-2r
- Proposition 13 Euclide Book II => OF^2=OC^2+CF^2+2 OC CC’
- (6-r)^2=(3)^2+(3+r)^2+2(3)n
- 36-12r+r^2=9+9+6r+r^2+6n
- 18-6n=18r
- 3-n=3r
- n=3-3r
- OD’FC’ is a rectangle=>
- OC’^2+OD’^2=OF^2
- (3-n)^2+(4+m)^2=(6-r)^2
- (3+3r-3)^2+(4- 2r+2)^2=(6-r)^2
- (3r)^2+(6-2r)^2=(6-r)^2
- 9r^2+36-24r+4r^2=36-12r+r^2
- 12r^2-48r+36=0
- r^2-4r+3=0
- Delta=16-4×3=4
- r=(4+-2)/2
- r=3 or r=1
- If r=3 => m=-4 : cannot be negative
- Therefore r=1 => m=0 and n=0
- Therefore ODFC is a rectangle
CASE D : D in OD’ and C in OC’
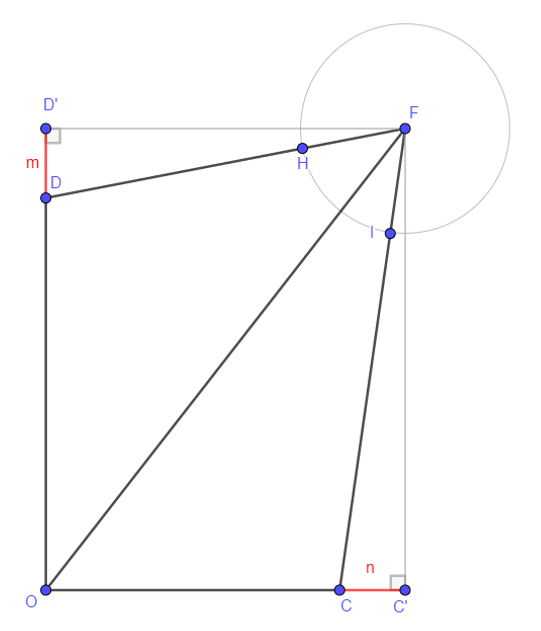
- Proposition 13 Euclide Book II => OF^2=OD^2+DF^2+2 OD DD’
- (6-r)^2=(4)^2+(2+r)^2+2(4)m
- 36-12r+r^2=16+4+4r+r^2+8m
- 16-8m=16r
- 2-m=2r
- m=2-2r
- Proposition 13 Euclide Book II => OF^2=OC^2+CF^2+2 OC CC’
- (6-r)^2=(3)^2+(3+r)^2+2(3)n
- 36-12r+r^2=9+9+6r+r^2+6n
- 18-6n=18r
- 3-n=3r
- n=3-3r
- OD’FC’ is a rectangle=>
- OC’^2+OD’^2=OF^2
- (3+n)^2+(4+m)^2=(6-r)^2
- (3-3r+3)^2+(4- 2r+2)^2=(6-r)^2
- (6-3r)^2+(6-2r)^2=(6-r)^2
- 36-36r+9r^2+36-24r+4r^2=36-12r+r^2
- 12r^2-48r+36=0
- r^2-4r+3=0
- Delta=16-4×3=4
- r=(4+-2)/2
- r=3 or r=1
- If r=3 => m=-4 : cannot be negative
- Therefore r=1 => m=0 and n=0
- Therefore ODFC is a rectangle
Conclusion : In all cases ODFC is a rectangle and r=1
There are many colinear points in this drawing :