From Gogeometry
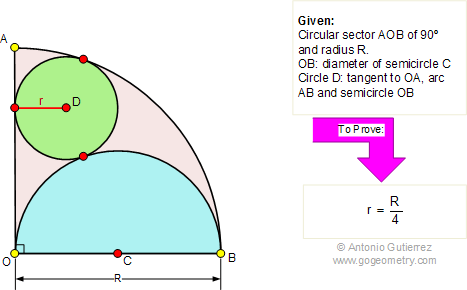

Using :
- Additional points
- Inscribed angles in a circle
- central and inscribed angle
- Tangents to a circle
- Inscribed angle and tangent to a circle
Without using :

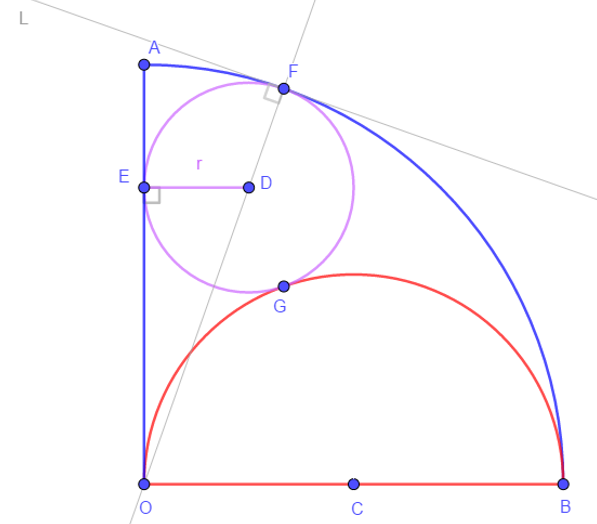
- Define :
- F the tangent intersection of CirleD and CircleO
- E intersection of CircleD and OA
- G intersection of CircleD and CircleC
- Define the line L tangent of CircleD and CircleO at F
- F in CircleO => OF ⊥ L, F in CircleD => DF ⊥ L
- => O, D and F are aligned
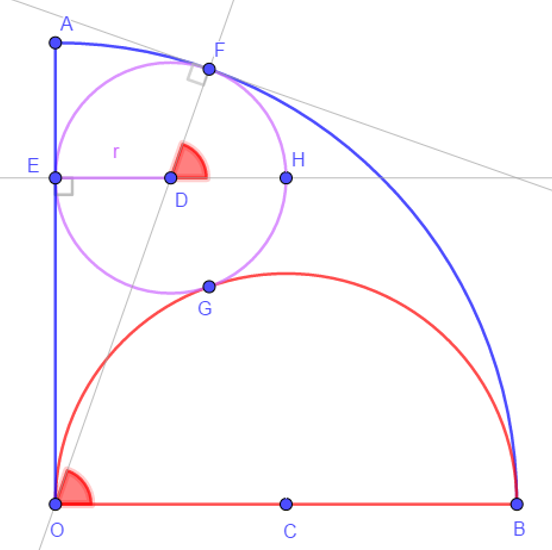
- Define H intersection of ED and CircleD
- ED⊥OA => ED//OB
- => ∠FDH=∠DOC
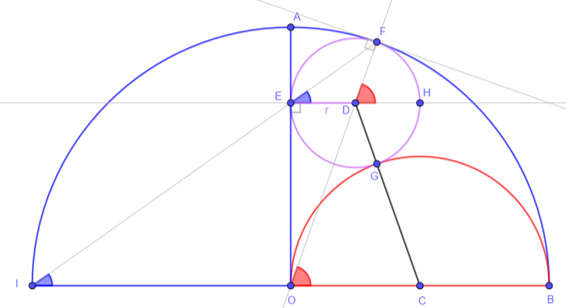
- Draw semi circle with center O and define I intersection of OB and the semi circle
- F and I on CircleO => ∠FOB=2 ∠FIB
- F and E on CircleD => ∠FDH=2 ∠FED
- ∠FDH=∠FOB => ∠FIB = ∠FED
- ∠FIB = ∠FED and ED//IO => F, E and I are aligned
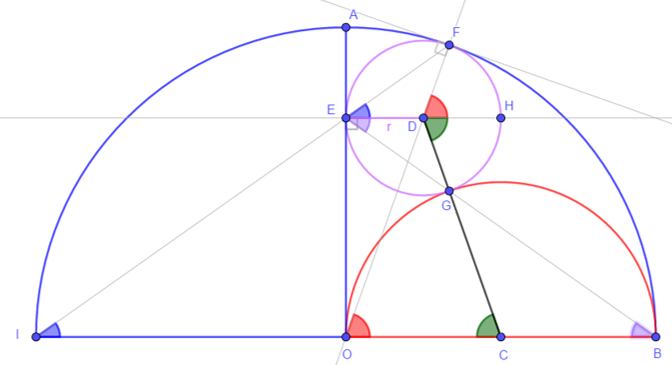
- D, G and C are aligned => ∠DCO = ∠CDH
- => ∠GED = ∠GBC
- ED//BC => E, G and B are aligned
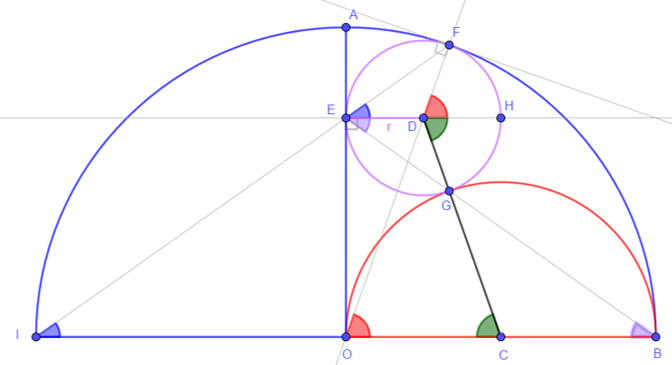
- OI=OB and OA⊥IB => ∠EIO = ∠EBO
- OB//ED =>∠EBO= ∠BED
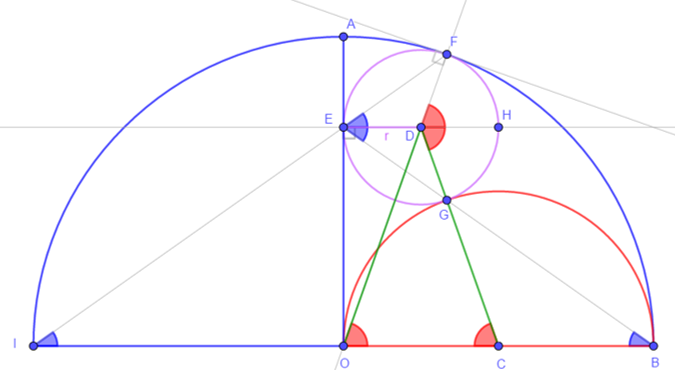
- => ∠GED=∠FED
- =>∠GDH=2∠GED and ∠GCO=2∠GBO
- ∠GED=∠FED => ∠DCO=∠DOC
- => ODC is isosceles => DO=DC
- DO=R-r and DC=r+R/2
- =>R-r=r+R/2
- =>R/2=2r
- Therefore r=R/4