Enigma

Enigmes & Problèmes scientifiques

Euclide Geometry Problem

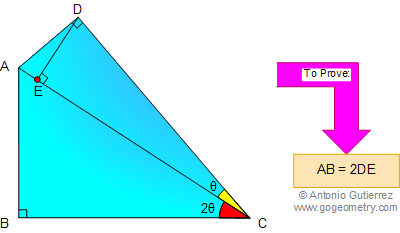
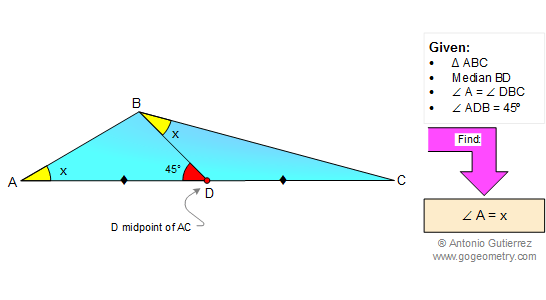
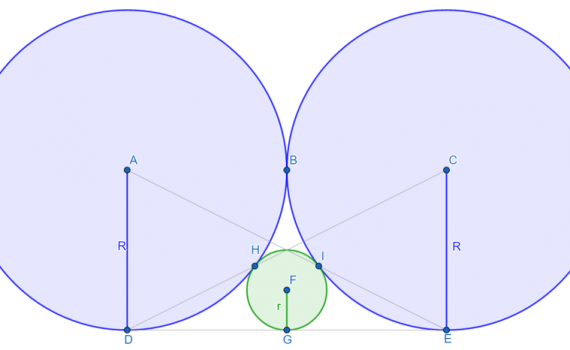
Using Additional points congruent triangles Area of a triangle [OQL]=OL . KL/2=bc/2[OPQ]+[LKQ]=PQ . KL/2+QK.KL/2=(PQ+QK).KL/2=PK.KL=bc/2=>[OQL]=[OPQ]+[LKQ]=bc/2[OPKL]= [OQL]+[OPQ]+[LKQ]=2bc/2=bc In the same way [LMHI]= [IJEF]= [FGNO]= [OPKL]= bc[QRST]= [OLIF] + [OQL] + [LRI] + [ISF] + [FTO][QRST]= c^2+2bc=c(c+2b) Therefore [QRST]= ac (Situation A) But, this is not true if b is too big, then […]

HP008

dans Euclide Geometry Problem / Géométrie Euclidienne étiqueté square par Harvey Littleman

From Gogeometry Using Additional points Inscribed angles in a circle central and inscribed angle congruent triangles Concyclic points ∠ABC=∠ADC = π/2 => ABCD are concyclic with center O=> OA=OD=OC=OB Define D’ such as ΔCAD is congruent to ΔCAD’∠CDA=∠CD’A = π/2 =>D’ is on the circle O=> ∠ACD= ∠ACD’= α => […]

Gogeometry Problem 017

dans Euclide Geometry Problem / Géométrie Euclidienne étiqueté Altitude / Auxiliary Lines / Double Angle / Right triangles par Harvey Littleman

From Gogeometry Using Additional points Inscribed angles in a circle congruent triangles Thales theorem Concyclic points ∠DBC = ∠DBA+∠ABC = π/2+∠ABC∠ABG = ∠ABC+∠BCG = ∠ABC+ π/2=> ∠DBC = ∠ABG=> Δ DBC is congruent to Δ ABG (SAS)=> ∠BDC = ∠BAG and DC=AG Define K the intersection of AG and BC=> […]

Gogeometry Problem 497

dans Euclide Geometry Problem / Géométrie Euclidienne étiqueté 90 Degrees par Harvey Littleman

From Gogeometry Using Additional points Pythagoras congruent triangles Similar triangles Equilateral triangle Let b=AD=DC and d=BCΔACB and ΔBCD are similar since ∠BAC=∠DBC=x and ∠BCD=∠BCAThen AC/BC=CB/CD=AB/BD => 2b/d=d/b => d=b√2 Define C’ such as DC’ ⊥ AC and DC’=b∠BDC=∠ADC – π/4= π – π/4 = 3 π/4∠BDC’=∠BDA + ∠ADC’ = π/4 […]

Gogeometry Problem 001

dans Euclide Geometry Problem / Géométrie Euclidienne étiqueté 45 Degrees / Angles / Congruence / Midpoint / Triangle par Harvey Littleman

From Gogeometry Using Additional points Inscribed angles in a circle congruent triangles Concyclic points Solution of a previous problem : 496 CK⊥ KH and CE⊥ EH =>CKEHJ are concyclic=> ∠EKC= 3Π/2= ∠EKJ + ∠JKC = ∠EKJ + ∠JEC = ∠EKJ + Π/2=> ∠EKJ= Π/2K and I on GJ, IE⊥ GJ […]

Gogeometry Problem 1291

dans Euclide Geometry Problem / Géométrie Euclidienne étiqueté Collinear Vertices / Midpoint / Three Squares par Harvey Littleman

From Gogeometry Using : Additional points Similar triangles •ΔABC is isosceles and right in B => BA=BC and ∠BAC=∠BCA=Π/4 • Define G in AC such as AB=AG => ΔBAG is isosceles in A •Define H intersection of AD and BG •∠BAH=∠GAH=Π/4/2=Π/8 and HB=HG and ∠AHB=∠AHG=Π/2 •and ∠ABH=∠AGH and ∠ABH+ ∠BAH […]

Gogeometry Problem 975

dans Euclide Geometry Problem / Géométrie Euclidienne étiqueté 45 Degrees / Angle Bisector / Hypotenuse / Isosceles Right Triangle par Harvey Littleman

From Gogeometry Using : Additional points Tangents to a circle •(1) AF=ra=r+EB+BF=r+a2 •(2) AG=ra=r+DC+CG=r+a1 •(1-2) a1=a2 •(1+2) ra=r+a1=r+a2 => a1=a2=ra-r •Define X as the intersection of BC and circle ra •Define Y as the intersection of BC and circle r •CD and CY tangents to circle r => CD=CY •BE […]

Gogeometry Problem 207

dans Euclide Geometry Problem / Géométrie Euclidienne étiqueté Exradius relative to the hypotenuse par Harvey Littleman

From Gogeometry Using : Isometric transformation Inscribed angles in a circle Equilateral triangle Tangents to a circle Define R radius of circle O and r radius of circle Q By construction and symmetry A, O, Q, D are collinear DE=DF, AE=AF AD angle bisector of ∠BAC D symmetric of A […]

Gogeometry Problem 1362

dans Euclide Geometry Problem / Géométrie Euclidienne étiqueté Equilateral Triangle Inscribed in a Circle / Lunula / Ratio of Areas / Sketch / Tangent par Harvey Littleman

Using : Additional points Pythagoras Similar triangles Thales theorem Tangents to a circle

Problem H003

dans Euclide Geometry Problem / Géométrie Euclidienne étiqueté circle par Harvey Littleman

From Gogeometry Using : Pythagoras Inradius in right triangle Define r as the inradius of ΔABC in a right triangle, r=(AB+BC-AC)/2 AB=AC => r=(2AB-AC)/2=AB-AC/2 BI=r.sqrt(2)=sqrt(2)(AB-AC/2)=sqrt(2).AB-AC/sqrt(2) AC=sqrt(2).AB => BI=AC-AB Therefore AC=AB+BI

Problem 976

dans Euclide Geometry Problem étiqueté 45 Degrees / Angle Bisector / Hypotenuse / Incenter / Isosceles Right Triangle par Harvey Littleman