Gogeometry Problem 284

 dans Euclide Geometry Problem par Harvey Littleman

---

From Gogeometry

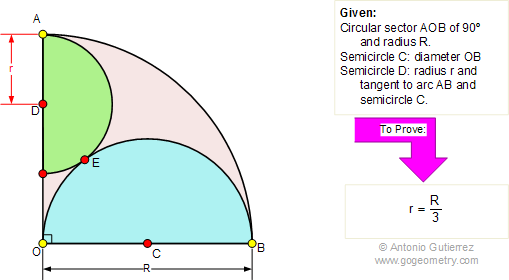
Using :

• Pythagoras

 

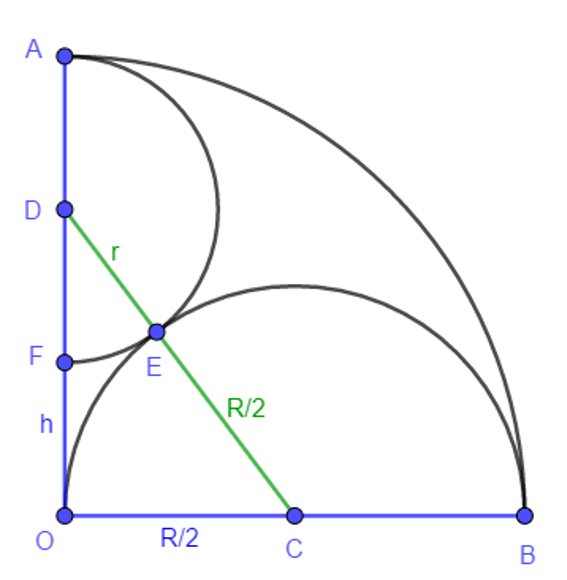
• Define h=OF
• OA=OB=R
• D, E and C are aligned
• ΔCOD is right in O => DC^2=OC^2+OD^2
• OD=r+h
• => (1) : (r+R/2)^2=(R/2)^2+(r+h)^2
• => (1) : (r+R)^2=R^2+4(r+h)^2
• OB=OA => R=2r+h => r+h=R-r
• (1) : (r+R)^2=R^2+4(R-r)^2
• => r^2+2rR+R^2=R^2+4(R^2-2rR+r^2)
• => 6rR= 3r^2
• Therefore 3R=r

---

---