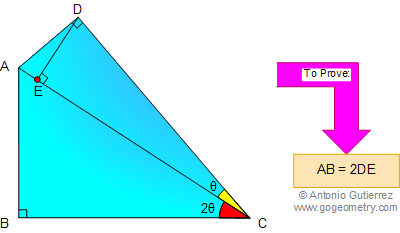
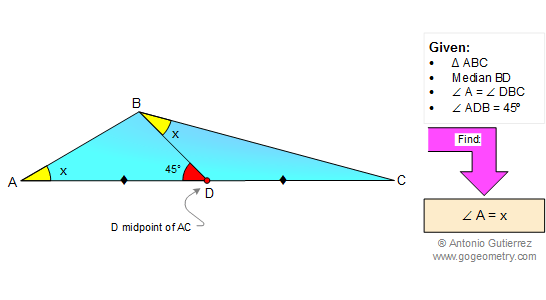
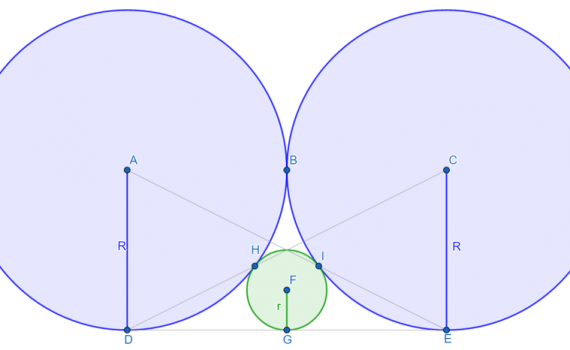
From Gogeometry Using Additional points congruent triangles Tangents to a circle Inscribed circle of a triangle Kite GN=GK=rg, DK and DN tangent to CircleG=> DK=DNFL=FM=rf, DL and DM tangent to CircleF=> DL=DMF center of circleF => F is on the angle bisector of ∠ADB=> ∠FDA= ∠FDB=xG center of circleG => […]