Gogeometry Problem 001

 dans Euclide Geometry Problem / Géométrie Euclidienne  étiqueté 45 Degrees / Angles / Congruence / Midpoint / Triangle par Harvey Littleman

---

From Gogeometry

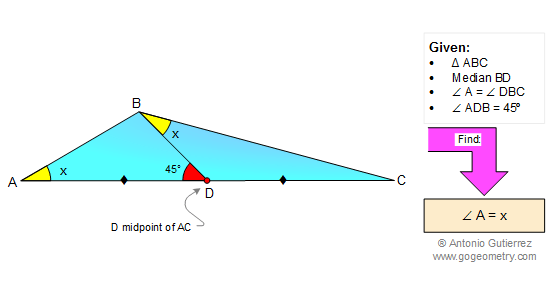
Using

• Additional points
• Pythagoras
• congruent triangles
• Similar triangles
• Equilateral triangle

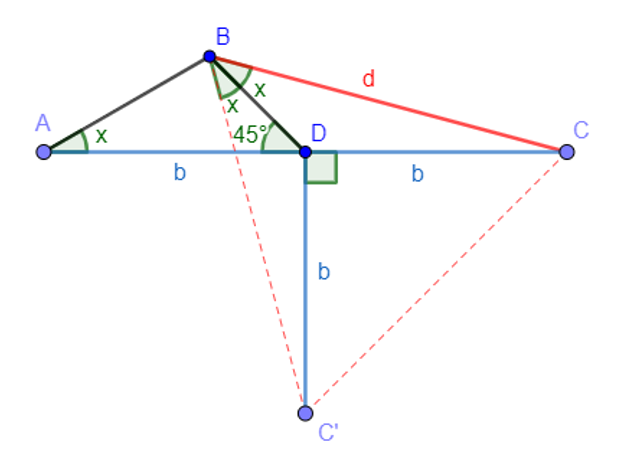
Let b=AD=DC and d=BC
ΔACB and ΔBCD are similar since ∠BAC=∠DBC=x and ∠BCD=∠BCA
Then AC/BC=CB/CD=AB/BD => 2b/d=d/b => d=b√2

Define C’ such as DC’ ⊥ AC and DC’=b
∠BDC=∠ADC – π/4= π – π/4 = 3 π/4
∠BDC’=∠BDA + ∠ADC’ = π/4 + π/2 = 3 π/4
=> ∠BDC= ∠BDC’

=>Δ BDC is congruent to ΔBDC’
=>BC=BC’=d and ∠DBC’=∠DBC=x => ∠C’BC=2x

DC’ ⊥ DC and DC’=DC=b => CC’ = b√2=d
ΔBCC’ is equilateral
∠C’BC = 60°=2x

Therefore  x=30°

---

---