From Gogeometry
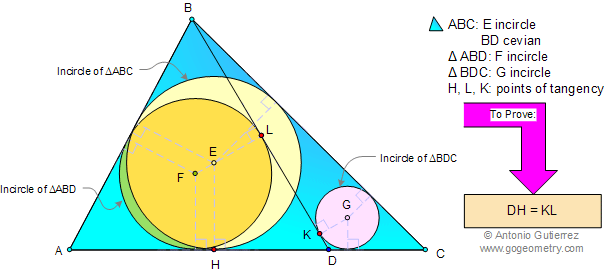

Using

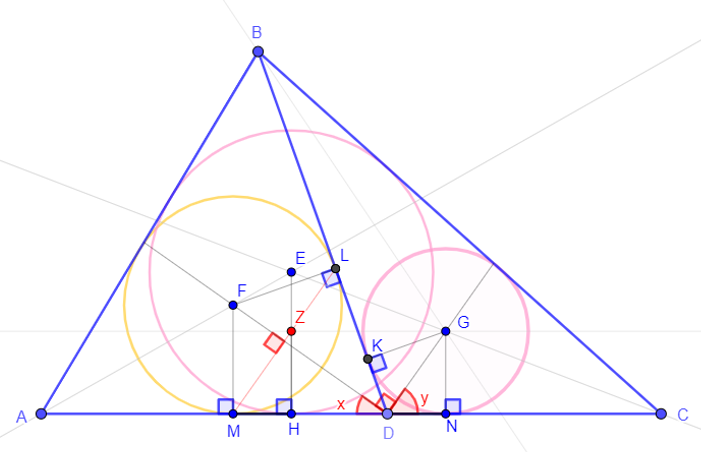
GN=GK=rg, DK and DN tangent to CircleG=> DK=DN
FL=FM=rf, DL and DM tangent to CircleF=> DL=DM
F center of circleF => F is on the angle bisector of ∠ADB=> ∠FDA= ∠FDB=x
G center of circleG => G is on the angle bisector of ∠BDC=> ∠GDB= ∠GDC=y
∠ ADC= π =2x+2y => x+y= π/2 => ∠GDF=π/2
=>DG ⊥ DF
DM=DL and FL=FM => DMFL is a kite=>ML ⊥ FD
Draw a line parallel to AB and passing through G
Define Z the intersection of this line and HE
ML ⊥ FD, Z on ML => MZ ⊥ FD
DG ⊥ FD => MZ//DG => ∠ZMH = ∠GDN
∠ZMH = ∠GDN and ∠MHZ = ∠DNG and HZ=NG =>ΔMHZ is congruent to ΔDNG
= >MH=DN
DL=DM => DK+KL=DH+HM =>DN+KL=DH+DN
Therefore LK=HD