Problem H003

 dans Euclide Geometry Problem / Géométrie Euclidienne  étiqueté circle par
Find r
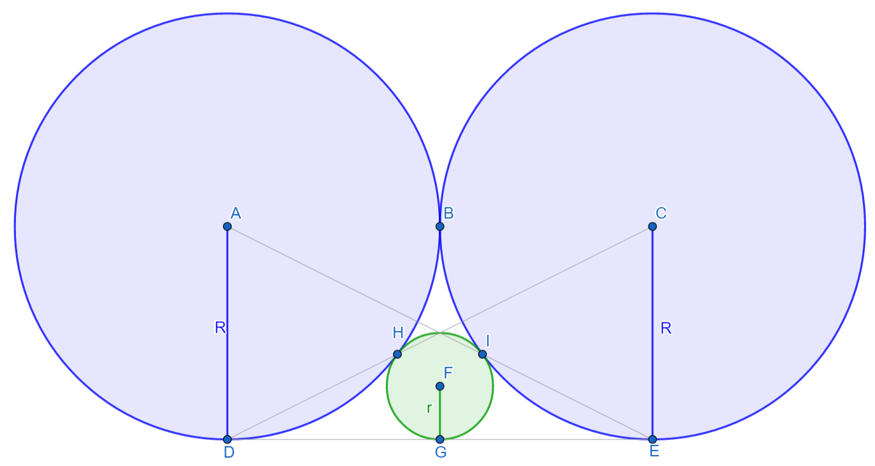
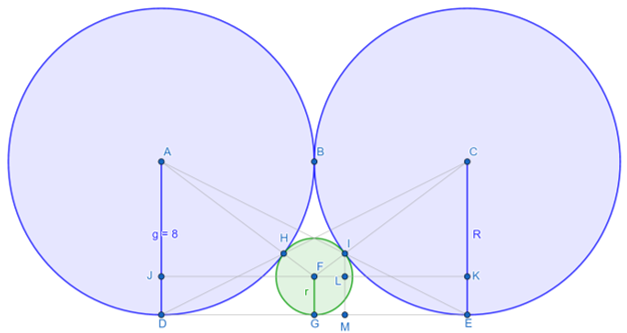
Prove : AIE and DHC are colinear
Solution

Using :

Solution
•Define J in AD and K in CE such as JK // DE
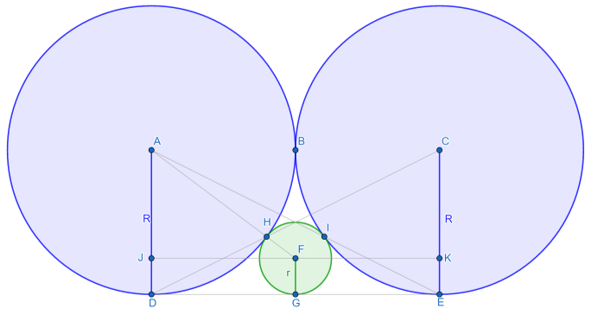
•In ΔAFJ : JA^2+JF^2=AF^2
•(R-r)^2+R^2=(R+r)^2
•R^2=(R+r)^2-(R-r)^2
•R^2=4rR Therefore r=R/4
•Define L in FK such as FK ⊥ LI
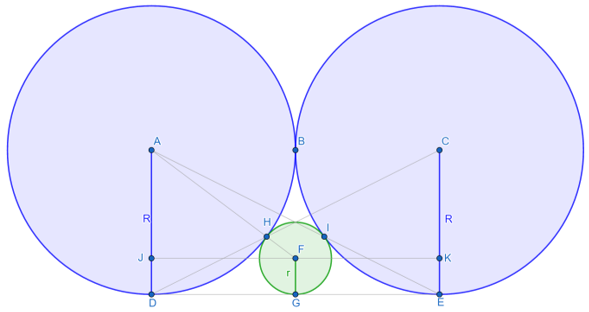
•ΔFLI is similar to ΔFKC =>IL/IF=CK/CF
•CK=R-r=3R/4 ; CF=R+r=5R/4 ; IF=r=R/4
IL=CK.IF/CF=(3R/4)r/(5R/4)=3Rr/5R=3r/5 => IL=3R/20
•FI^2=FL^2+LI^2
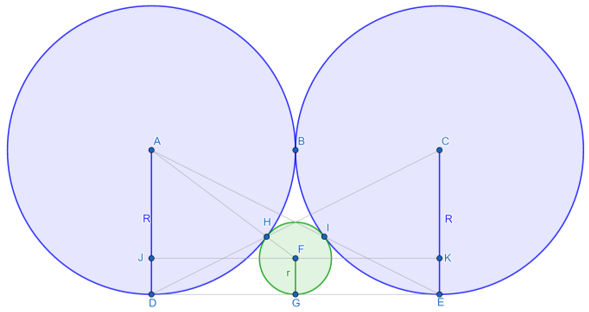
•r^2=FL^2+(3r/5)^2
•FL^2=r^2-9r^2/25=16r^2/25
•Therfore FL=4r/5=R/5
•Define M in DE such as JK ⊥ IM
•GM=FL
•IM=(IL+LM)=3R/20 + r= 3R/20 + R/4=8R/20=2R/5=IM
•ME=GE-GM=R-R/5=4R/5=ME
•IM/ME=(2R/5)/(4R/5)=1/2
•AD/DE=R/2R=1/2
•Therefore IM/ME = AD/DE
•M in DE => AIE are collinear (reverse Thales)

Laissez un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *