Gogeometry Problem 017

 dans Euclide Geometry Problem / Géométrie Euclidienne  étiqueté Altitude / Auxiliary Lines / Double Angle / Right triangles par Harvey Littleman

---

From Gogeometry

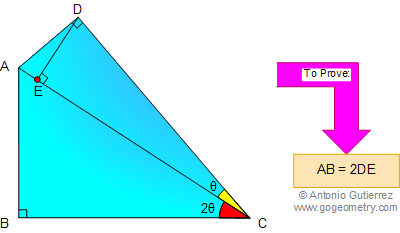
Using

• Additional points
• Inscribed angles in a circle
• central and inscribed angle
• congruent triangles
• Concyclic points

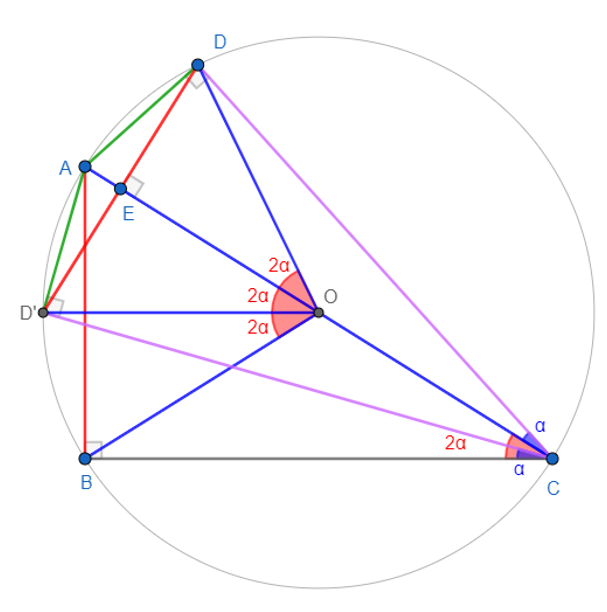
∠ABC=∠ADC = π/2 => ABCD are concyclic with center O
=> OA=OD=OC=OB

Define D’ such as ΔCAD is congruent to ΔCAD’
∠CDA=∠CD’A = π/2 =>D’ is on the circle O
=> ∠ACD= ∠ACD’= α => ∠BCD’= α
=>ΔECD is congruent to ΔECD’ (SAS) => ED=ED’

∠ACD= ∠ACD’= ∠BCD’= α => ∠AOD= ∠AOD’= ∠BOD’= 2α
∠DOD’= ∠AOB= 4α =>ΔDOD’ is congruent to ΔAOB (SAS)
=> DD’=AB

DD’=2DE
Therefore AB=2 DE

---

---