From Gogeometry


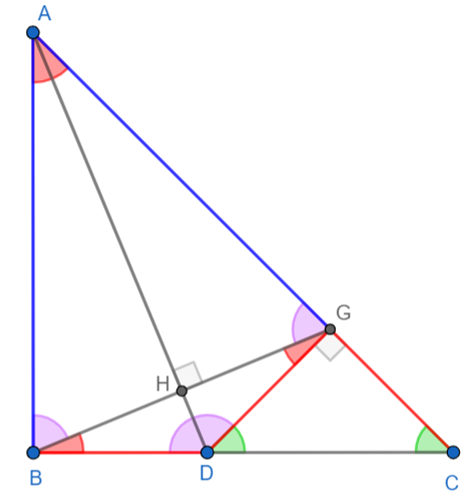

Using :

•ΔABC is isosceles and right in B => BA=BC and ∠BAC=∠BCA=Π/4 • Define G in AC such as AB=AG => ΔBAG is isosceles in A •Define H intersection of AD and BG •∠BAH=∠GAH=Π/4/2=Π/8 and HB=HG and ∠AHB=∠AHG=Π/2 •and ∠ABH=∠AGH and ∠ABH+ ∠BAH =∠AGH + ∠GAH =Π/2 •∠ABD= ∠ABH+ ∠HBD =Π/2 => ∠HBD= ∠BAH •=> ∠AGD= Π/2 •In ΔDGC, ∠AGD= Π/2 and ∠GCD= Π/4 => ∠GDC= Π/4 •=> ΔDGC is isosceles => GD=GC •But GD=BD => GC=BD •AC=AG+GC •Therefore AC=AB+BD