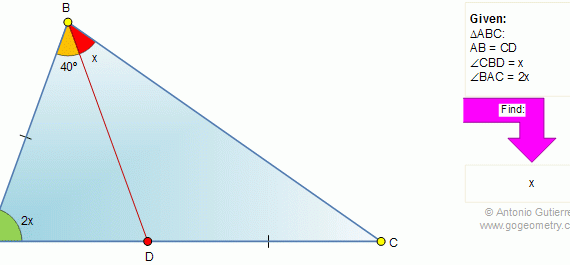
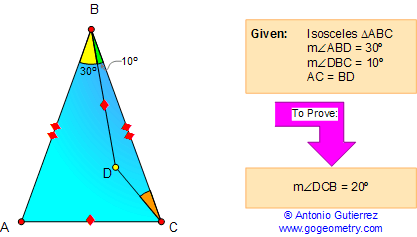
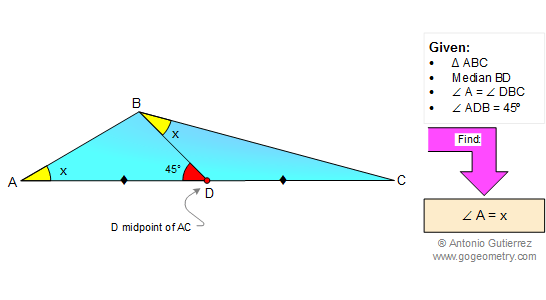
From Gogeometry Using Additional points Inscribed angles in a circle congruent triangles Concyclic points
Congruence
From Gogeometry Using Inscribed angles in a circle Equilateral triangle Concyclic points ∠BAD= π/2 => B, A and D are concyclic, circle with center F middle of BD=> FB=FA=FD and ∠BAF=15°In the same way, GC=GA=GE and ∠CAG=15°=>∠FAG=90-15-15=60°ΔFAG is isosceles in A (AF=AG) and ∠FAG=60° => ΔFAG is equilateral Therefore x=FG=BD/2=CE/2=1
Gogeometry Problem 406
From Gogeometry Using Additional points congruent triangles Equilateral triangle Thales theorem ∠ABC = 30°+10°=40°Define F on AC and on the angle bisector of <ABCΔABC isosceles in B => ∠ABF=∠FBC = 40°/2=20°Define I such as ΔAIC is equilateral => ∠IAC=60°ΔABC isosceles in B => ∠ABI=∠CBI = 20°∠ABC = 40° and ΔABC […]
Gogeometry Problem 60
From Gogeometry Using Additional points Pythagoras congruent triangles Similar triangles Equilateral triangle Let b=AD=DC and d=BCΔACB and ΔBCD are similar since ∠BAC=∠DBC=x and ∠BCD=∠BCAThen AC/BC=CB/CD=AB/BD => 2b/d=d/b => d=b√2 Define C’ such as DC’ ⊥ AC and DC’=b∠BDC=∠ADC – π/4= π – π/4 = 3 π/4∠BDC’=∠BDA + ∠ADC’ = π/4 […]