Enigma

Enigmes & Problèmes scientifiques

Harvey Littleman

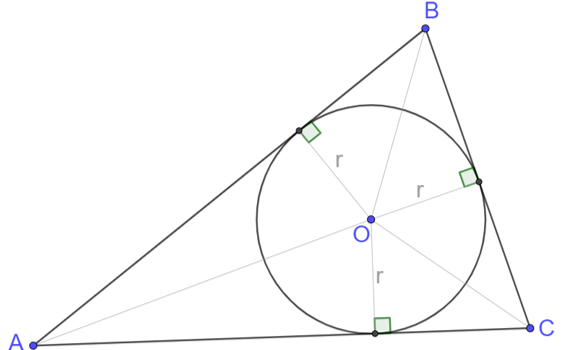
From Gogeometry Using : Pythagoras Inradius in right triangle Define r as the inradius of ΔABC in a right triangle, r=(AB+BC-AC)/2 AB=AC => r=(2AB-AC)/2=AB-AC/2 BI=r.sqrt(2)=sqrt(2)(AB-AC/2)=sqrt(2).AB-AC/sqrt(2) AC=sqrt(2).AB => BI=AC-AB Therefore AC=AB+BI

Problem 976

dans Euclide Geometry Problem étiqueté 45 Degrees / Angle Bisector / Hypotenuse / Incenter / Isosceles Right Triangle par Harvey Littleman

ΔABC right triangle in C Define r its inradius, a=BC,b=AC and c=A PCRO is square => PC=CR=r AC et AB tangents to the circle=>AP=AQ, BQ=BR and CP=CR b=AC=AP+PC, a=BC=BR+RC AC+BC=b+a=AP+r+BR+r=2r+AP+BR AP=AQ, BR=BQ => AC+BC=b+a=2r+AQ+BQ=2r+AB=2r+c a+b=2r+c Therefore r=(a+b-c)/2 Define p as the semi-perimeter of the triangle, p=(a+b+c)/2 Therefore r =p-c

Inradius in right triangle

dans Euclide Geometry Principles par Harvey Littleman

define a CB, b=AC and c=AB Define S as the area of the triangle S=r.a/2 + r.b/2 + r.c/2 Therefore S=r(a+b+c)/2 and r=2S/(a+b+c)

Inscribed circle of a triangle

dans Euclide Geometry Principles par Harvey Littleman

From Gogeometry Define a=AB=BC=AC DC and DB tangents to Circle O1 => DG=DE=bAD and AB tangents to Circle O1 => AG=AJ=dDB and BA tangents to Circle O1 => BE=BJ=c DB and BC tangents to Circle O2 => BF=BK=eDC and BC tangents to Circle O2 => CI=CK=f a=d+c=e+fDF=b+c+e, DI=b+d+a+fDC and DB […]

Gogeometry Problem 1372

dans Euclide Geometry Problem étiqueté Altitude / Equilateral Triangle / Exradius / Exterior Cevian / Inradius par Harvey Littleman

From Gogeometry Using : Additional points Similar triangles Equilateral triangle Define 0 middle of BC. O is the center of semicircle OD diameter BC Define a=OB=OD=OC => AB=AC=BC=2a Arc BD=arc DE=arc EC => ∠BOD=∠DOE=∠EOC=Π/3 OB=OD=a and ∠BOD=Π/3 =>BD=a, ΔBOD is equilateral and BD//AC In the same way, DE=a, ΔDOE […]

Gogeometry Problem 326

dans Euclide Geometry Problem étiqueté Equal arcs par Harvey Littleman

From Gogeometry Using : Pythagoras Proposition 13 Euclide Book II In ΔDMF : DM^2=DF^2+FM^2 (1) DM^2= (r-x/2)^2+x^2 In ΔAMD : AM^2=AD^2+DM^2 -2xAD (Proposition 13 Euclide Book II) r^2= r^2+ DM^2 -2xr (2) DM^2=2xr (1) and (2) 2xr=(r-x/2)^2+x^2 2xr=r^2-xr+x^2/4+x^2 3xr=r^2+5x^2/4 Dividing by x^2 (x not equal to 0) =>3r/x=5/4+(r/x)^2 Let y=r/x […]

Gogeometry Problem 336

dans Euclide Geometry Problem étiqueté a Common Tangent and a Square / Two equal circles par Harvey Littleman

From Gogeometry Using : Isometric transformation Additional points Pythagoras Similar triangles Tangents to a circle Define O middle of AB, r=ED AD^2+AO^2=DO^2 a^2+(a/2)^2=(a/2+r)^2 a^2+a^2/4=a^2/4+r^2+ar r^2+ar-a^2=0 ∆=a^2+4a^2=5a^2 r>0 => r=(a.sqr(5)-a )/2 Draw a square symetryc of ABCD by O =>D becomes D’, C becomes C’, E becomes E’ => C’D’BA is […]

Gogeometry Problem 458

dans Euclide Geometry Problem étiqueté Circular Sector / Internal Common Tangent / Measurement / Semicircle / square par Harvey Littleman

From Gogeometry Using : Additional points Pythagoras Solution of a previous problem Tangents to a circle Proposition 13 Euclide Book II R radius of CircleO, and r of CircleF Define ro radius of CircleO , rd of CircleD, rc of CircleC and rf of CircleF Define G intersection of OA […]

Gogeometry Problem 285

dans Euclide Geometry Problem par Harvey Littleman

CircleO1 intersects CircleO2 in A and B By symmetry, CA=CB O2A=O2B => Δ AO2B is isosceles in O2 =>AC ⊥ CO2 In the same way with CircleO1: O1O2⊥ AB

Intersection of two circles

dans Euclide Geometry Principles par Harvey Littleman

From Gogeometry Using : Pythagoras Define h=OF OA=OB=R D, E and C are aligned ΔCOD is right in O => DC^2=OC^2+OD^2 OD=r+h => (1) : (r+R/2)^2=(R/2)^2+(r+h)^2 => (1) : (r+R)^2=R^2+4(r+h)^2 OB=OA => R=2r+h => r+h=R-r (1) : (r+R)^2=R^2+4(R-r)^2 => r^2+2rR+R^2=R^2+4(R^2-2rR+r^2) => 6rR= 3r^2 Therefore 3R=r

Gogeometry Problem 284

dans Euclide Geometry Problem par Harvey Littleman