From Gogeometry
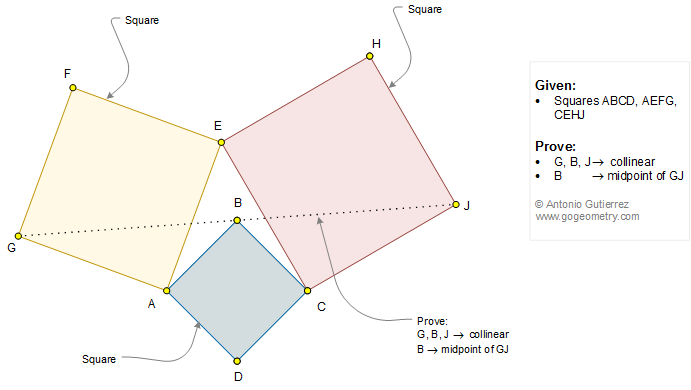

Using
- Additional points
- Inscribed angles in a circle
- congruent triangles
- Concyclic points
- Solution of a previous problem : 496

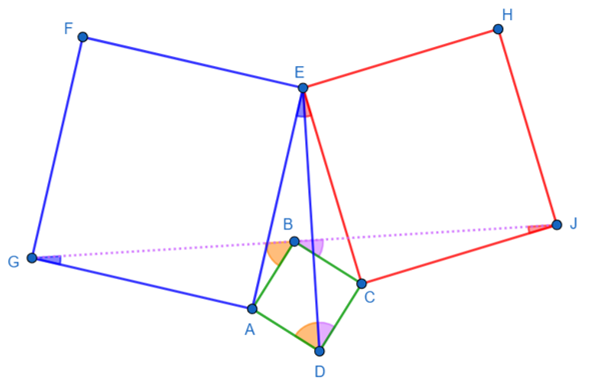
∠GAB= ∠GAE+∠EAB=Π/2+∠EAB
∠EAD= ∠EAB+ ∠BAD=∠EAB+ Π/2
=> ∠GAB= ∠EAD
=> ΔGAB is congruent to ΔEAD (SAS)
=> GB=ED
=> ∠GBA= ∠EDA
In the same way, ΔJCB is congruent to ΔECD (SAS)
=>JB=ED
=> ∠CBJ= ∠EDC
GB=ED and JB=ED Therefore BG=BJ
∠ADC= Π/2=∠ADE+∠EDC
∠GBJ = ∠GBA +∠ABC+∠CBJ= ∠ADE+Π/2 +∠EDC= Π
Therefore G,B and J are aligned

Define I intersection of GJ and ED
∠CJI= ∠CEI => CJIE are concyclic
=> ∠ECJ= ∠EIJ => ∠EIJ = Π/2
Therefore GJ ⊥DE
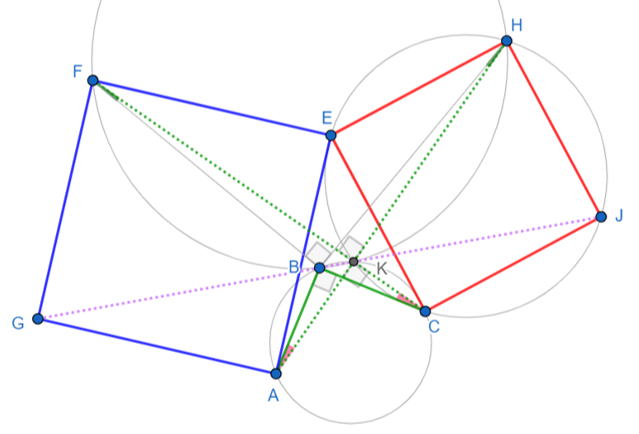
From problem 496 : CF=AH, CF⊥ AH and CF AH and GJ are concurrent (K)
CF⊥ AH => KF⊥ KH => FH diameter of circle FKH
∠AKC= ∠ABC = Π/2
=>ABKC are concyclic
=> ∠BAK= ∠BCK
=> ∠BAH= ∠BCF
Δ BAH is congruent to Δ BCF (SAS)
=> BH=BF and ∠BHA= ∠BFC
=> ∠BHK= ∠BFK
=>FBKH are concyclic
KF⊥ KH Therefore BF⊥ BH

CK⊥ KH and CE⊥ EH =>CKEHJ are concyclic
=> ∠EKC= 3Π/2= ∠EKJ + ∠JKC = ∠EKJ + ∠JEC = ∠EKJ + Π/2
=> ∠EKJ= Π/2
K and I on GJ, IE⊥ GJ and KE⊥ GJ
Therefore K=I