Enigma

Enigmes & Problèmes scientifiques

Harvey Littleman

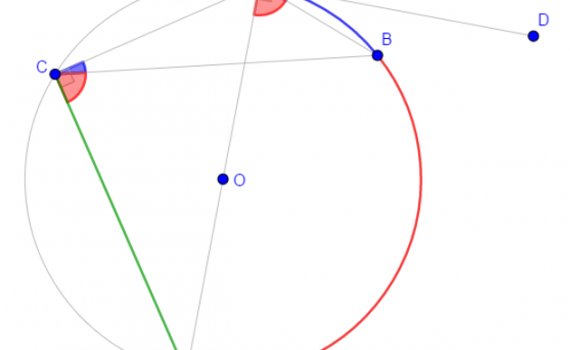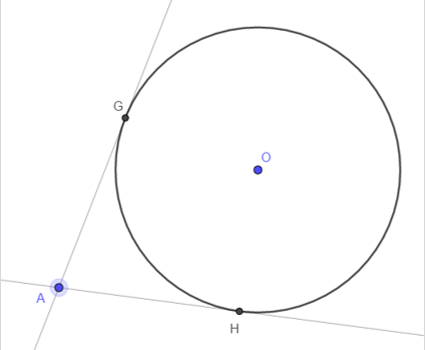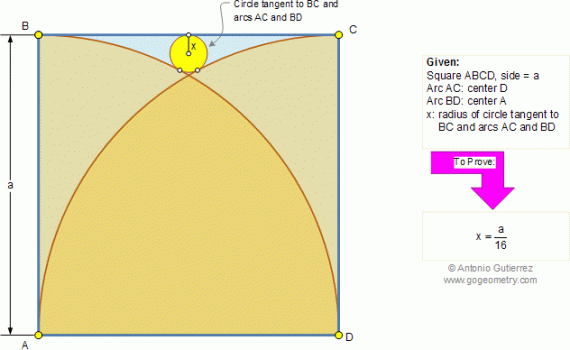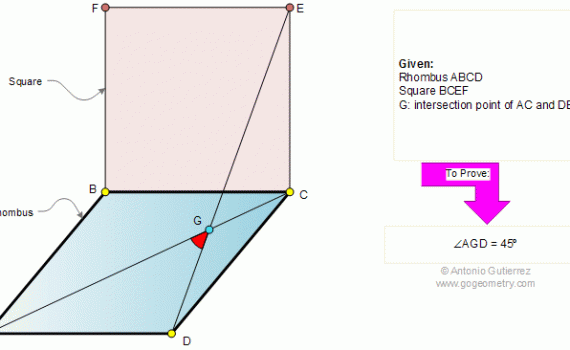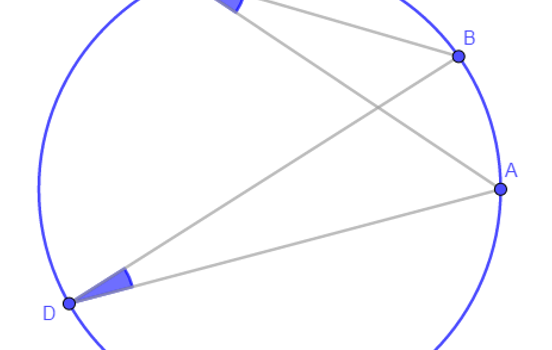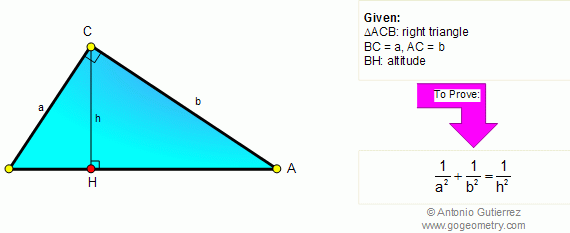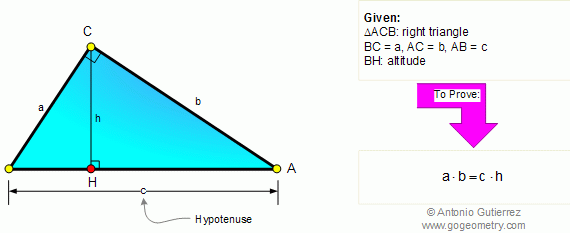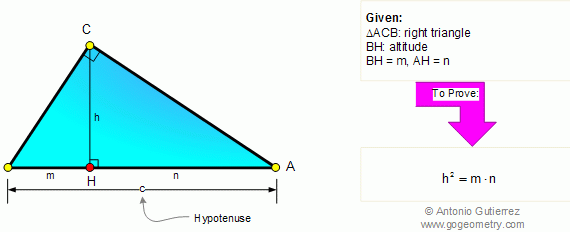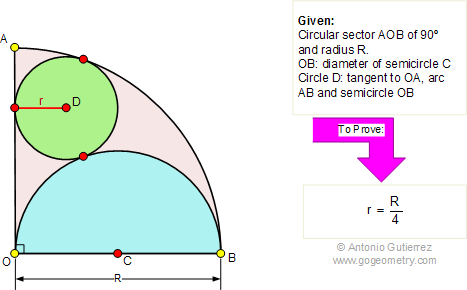
From Gogeometry Using : Additional points Inscribed angles in a circle central and inscribed angle Tangents to a circle Inscribed angle and tangent to a circle Without using : Law of cosines Define : F the tangent intersection of CirleD and CircleO E intersection of CircleD and OA G intersection […]

Gogeometry Problem 283

dans Euclide Geometry Problem par Harvey Littleman

Define h=HB Case 1) H in AC a^2=h^2+(b-m)^2 c^2=h^2+m^2 a^2-c^2=b^2-2mb Therefore a^2=b^2+c^2-2mb Case 2) A in HC a^2=h^2+(b+m)^2 c^2=h^2+m^2 a^2-c^2=b^2+2mb Therefore a^2=b^2+c^2+2mb

Proposition 13 Euclide Book II (Law of Cosines)

dans Euclide Geometry Principles par Harvey Littleman

AD tangent to circle with center O C on this circle => ∠BAD= ∠BCA Demonstration Define E in the circle such as E, O and A are colinear ∠0AD=90° and ∠ECA= 90° ∠BAE intercepts arc BE and ∠BCE intercepts arc BE => ∠BAE= ∠BCE ∠0AD= ∠0AB+∠BAD=90° ∠ECA= ∠ECB+∠BCA=90° […]

Inscribed angle and tangent to a circle

dans Euclide Geometry Principles par Harvey Littleman

AG and AH are tangent to a circle with center O =>AG=AH Proof AG and AH are tangent to a circle with center O <=>∠AHO=∠AGO= π/2 OH=OG=r => O is at the same distance of AH and AG => O in on the angle bissector of ΔGAH => ∠GAO=∠HAO =>ΔOAG […]

Tangents to a circle

dans Euclide Geometry Principles par Harvey Littleman

From Gogeometry Using : Inscribed angles in a circle central and inscribed angle congruent triangles Similar triangles Tangents to a circle Inscribed angle and tangent to a circle Without using : Pythagoras Define G the center of CircleG with radius x Define the point E as the only point […]

Gogeometry Problem 276

dans Euclide Geometry Problem par Harvey Littleman

From Gogeometry Using : Inscribed angles in a circle congruent triangles Concyclic points ABCD is a rhombus => ΔACD is congruent to ΔACB => ∠ACD = ∠ACB => ΔGCD is congruent to ΔGCB (SAS) => ∠GDC = ∠GBC ABCD is a rhombus =>CE=CD => ΔDCE is isosceles in C => […]

Gogeometry Problem 354

dans Euclide Geometry Problem par Harvey Littleman

Points A, B, C and D on a circle <=> ∠ACB= ∠ADB

Concyclic points

dans Euclide Geometry Principles par Harvey Littleman

From Gogeometry Using : Pythagoras Area of a triangle Define c=AB S=[ABC]=a.b/2=c.h/2 => a.b=c.h c=a.b/h => c^2=a^2.b^2/h^2 Pythagoras => a^2+b^2=c^2 => a^2+b^2=a^2.b^2/h^2 dividing by a^2.b^2 => 1/b^2 + 1/a^2 = 1/h^2

Gogeometry Problem 268

dans Euclide Geometry Problem par Harvey Littleman

From Gogeometry Using : Pythagoras Area of a triangle S=[ABC] S=a.b/2 But also S=c.h/2 Therefore a.b=c.h

Gogeometry Problem 267

dans Euclide Geometry Problem par Harvey Littleman

From Gogeometry Using : Pythagoras (1) ΔABC : AC^2+BC^2=c^2 (2) ΔAHC : AC^2 =h^2+n^2 (3) ΔBHC : BC^2=h^2+m^2 c=m+n, c^2=(m+n)^2=m^2+n^2+2mn (1,2,3) h^2+n^2+h^2+m^2=m^2+n^2+2mn 2h^2=2mn Therefore h^2=m.n

Gogeometry Problem 266

dans Euclide Geometry Problem par Harvey Littleman