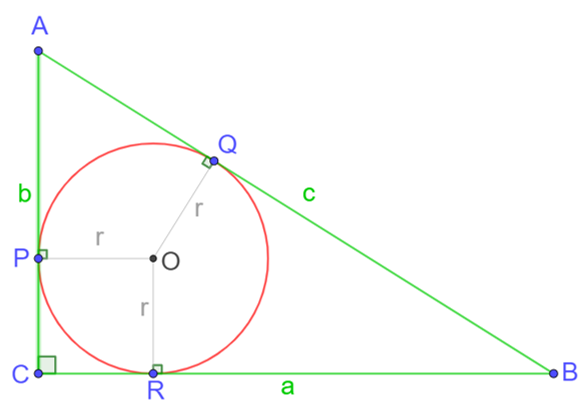
- ΔABC right triangle in C
- Define r its inradius, a=BC,b=AC and c=A
- PCRO is square => PC=CR=r
- AC et AB tangents to the circle=>AP=AQ, BQ=BR and CP=CR
- b=AC=AP+PC, a=BC=BR+RC
- AC+BC=b+a=AP+r+BR+r=2r+AP+BR
- AP=AQ, BR=BQ => AC+BC=b+a=2r+AQ+BQ=2r+AB=2r+c
- a+b=2r+c
- Therefore r=(a+b-c)/2
- Define p as the semi-perimeter of the triangle, p=(a+b+c)/2
- Therefore r =p-c