Gogeometry Problem 60

 dans Euclide Geometry Problem / Géométrie Euclidienne  étiqueté Congruence / Isosceles triangle par Harvey Littleman

---

From Gogeometry

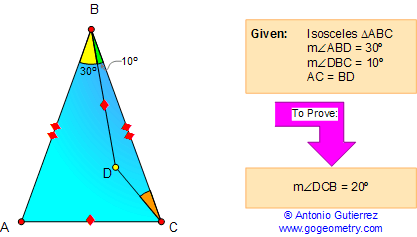
Using

• Additional points
• congruent triangles
• Equilateral triangle
• Thales theorem

∠ABC = 30°+10°=40°
Define F on AC and on the angle bisector of <ABC
ΔABC isosceles in B => ∠ABF=∠FBC = 40°/2=20°
Define I such as ΔAIC is equilateral => ∠IAC=60°
ΔABC isosceles in B => ∠ABI=∠CBI = 20°
∠ABC = 40° and ΔABC isosceles in B => ∠BAC=70°
∠BAI = ∠BAC – ∠IAC=70° – 60° =10°
AC=BD (given) and AC=AI=> ΔIAB is congruent to ΔDBC (SAS)

Therefore ∠ ABI = ∠ BCD = 20°

---

---