From Gogeometry

Using

• Pythagoras
• central and inscribed angle
• Equilateral triangle

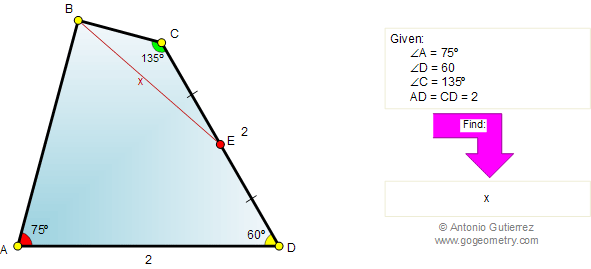
DC=DA and ∠ADC= π/3 => ΔADC is equilateral
∠CAD= π/3, ∠BAC+∠CAD=∠BAD=75° => ∠BAC=15°
∠ACD= π/3, ∠BCA+∠ACD=∠BCD=155° => ∠BCA=75°
∠BAC=15° et ∠BCA=75° => ∠ABC= π/2

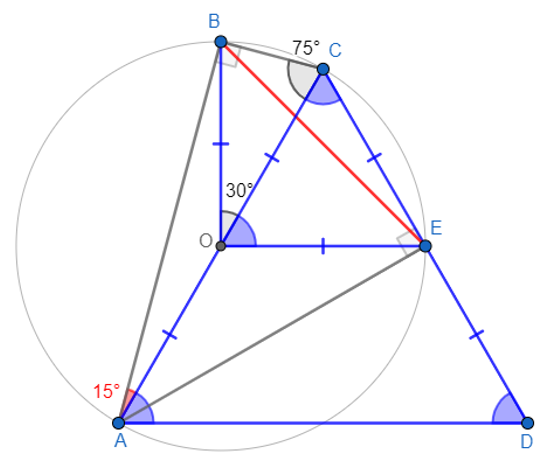
ΔADC is equilateral and EC=ED => ∠AEC= π/2
∠ABC= π/2 et ∠AEC= π/2 => A, B, C and E are concyclic with center O middle of AC => OA=OB=OC=OE=1
∠BAC=15° =>∠BOC=30° (Inscribed angle)
∠BOC=30°  and ∠COE= π/3 =>  ∠BOE= π/2
OE=OB=1 and ∠BOE= π/2

Therefore BE=sqrt(2)