From Gogeometry :

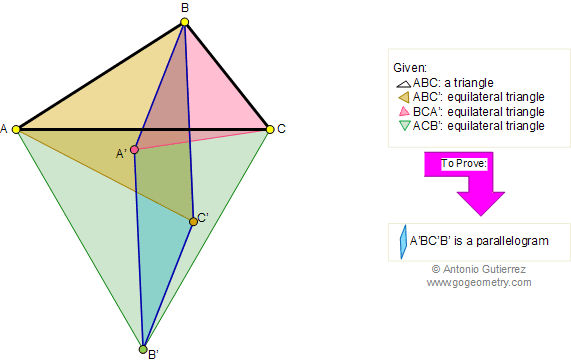
Using :

• Equilateral triangle
• Congruent triangles
• Parallelogram

• ΔCAB’ and ΔC’AB are equilateral
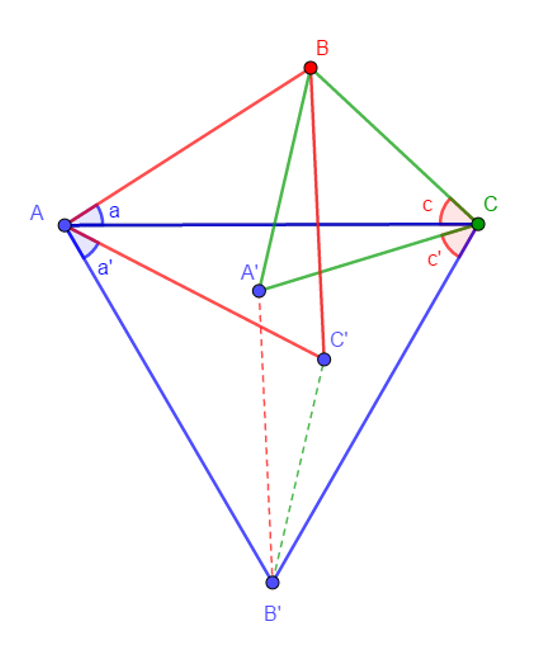
• => ∠CAB’=∠C’AB=Π/3
• ∠BAB’=a+∠CAB’=∠BAC’+a’
• => a=a’
• AC’=AB and AB’=AC and a=a’=> ΔBAC and ΔB’AC’ are congruent (SAS)
• =>B’C’=BC
• But BC=BA’=>B’C’=BA’
• In the same way : ∠BCA’=∠B’CA=Π/3
• ∠BCA=c= Π/3 – ∠ACA’
• ∠B’CA’=c’= Π/3 – ∠ACA’ =>c=c’
• CB=CA’ and CA=CB’ and c=c’=> ΔBCA and ΔA’CB’ are congruent (SAS)
• =>AB=A’B’
• But AB=BC’ => A’B’=BC’

• B’C’=BA’ and A’B’=BC’ => BA’B’C’ is a parallelogram