From Gogeometry :
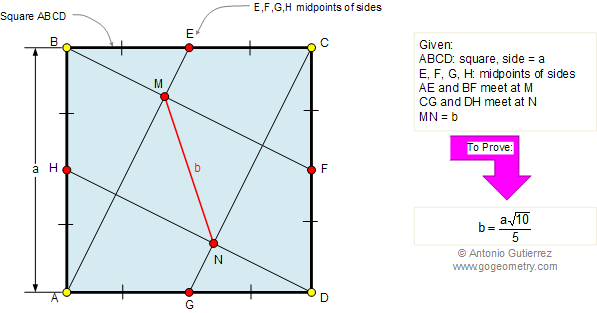

Using :

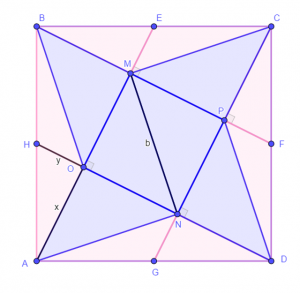
- Define O intersection of AE and HD and P intersection of BF and GC
- ABE is congruent to CBF by rotation of pi/2
- => <DNP=<FPC=<NOM=<PME=90°
- Define x=OA and y=OH
- Define S1=[AOH]= x y /2
- [AOH]= [HOB]= [BME]= [EMC]= [CPF]= [FPD]= [GND]= [GNA]=S1
- Define S2=[OMN]
- [OMN]= [PMN]= [OMB]= [MPC]= [PND]= [ONA]= S2= x^2/2
- S=[ABCD]= a^2 = 8 S1 + 6 S2 = 4 x y+ 3 x^2
- AO/OH=AM/MB => x = 2 y
- S= a^2 = 2 x^2+ 3 x^2 = 5 x^2
- =>x^2 = a^2/5
- b hypotenuse =>b^2= 2x^2 = 2a^2/5
- Therefore b^2 = 10 a^2/25