From Gogeometry

Using :

• Pythagoras
• Inscribed angles in a circle
• central and inscribed angle
• Concyclic points
• Solution of a previous problem : Pb367

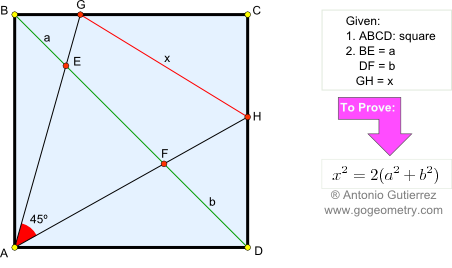
• AD⊥AH => A, D, H are concyclic
• Arc EH : ∠EDH=45° and ∠EAH=45° => A, D, H and E are concyclic
• Arc AE : ∠EDA=45° => ∠EHA=45° => EA⊥EH and EA=EH

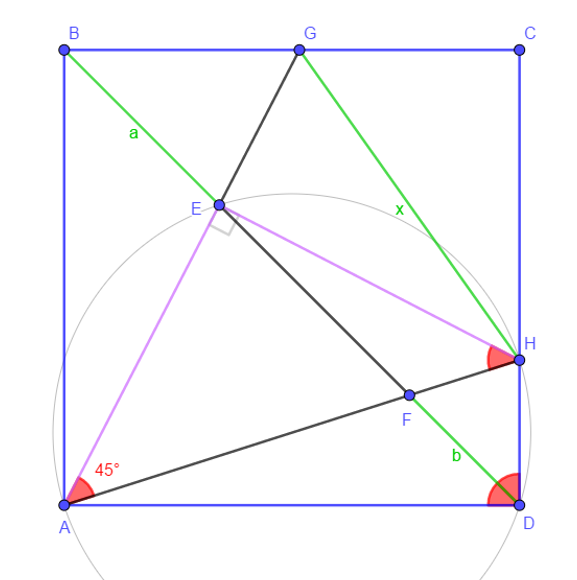
• AB⊥BG => A, B, G are concyclic
• Arc GF : ∠GBF=45° and ∠GAF=45° => A, B, G and F are concyclic
• Arc AG : ∠ABG=90° => ∠AFG=90° => FA⊥FG and FA=FG and AGF=45°

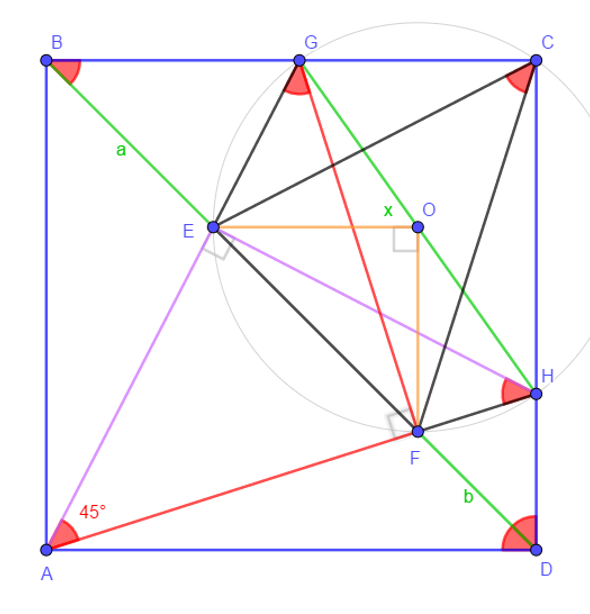
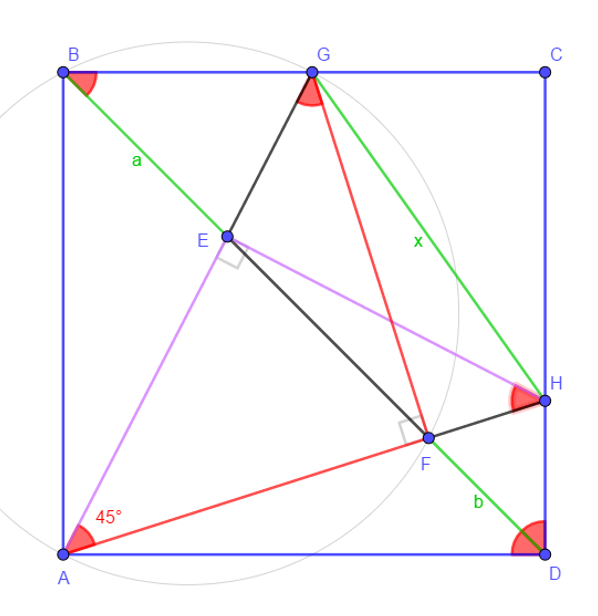
• CG⊥CH => C, G, H are concyclic with center O
• Arc GH : ∠GCH=90° and ∠GFH=90° => C, G, H and F are concyclic
• Arc EF : ∠EHF=45° and ∠EGF=45° => C, G, H, F and E are concyclic and ∠ECF=45°
• ∠ECF=45° => ∠EOF=90°
• A, B, G, F and E are concyclic => OG=OE=OF=OH=OC
• x=2OG=2OE
• EF^2=OE^2+OF^2=2OE^2=x^2/2
• From Pb 367 : EF^2=a^2+b^2
• => a^2+b^2= x^2/2
• Therefore x^2=2(a^2+b^2)