From Gogeometry
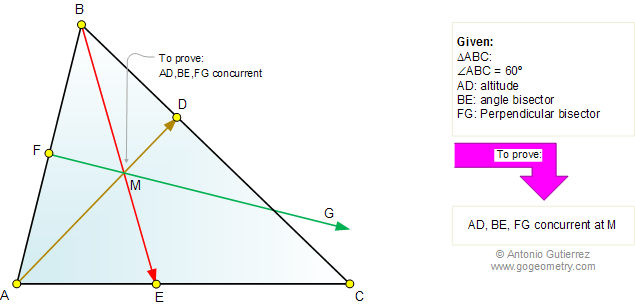

Using

•AD altitude => ∠BDA = π/2
•BE angle bisector =>∠ABE=∠CBE= π/6
•Define M as the intersection of BE and AD
•Define F on AB such as BF ⊥ FM
•Then we have to demonstrate that FB=FA to prove that FG is perpendicular bisector
•∠MBD= π/6 and ∠BDM = π/2 => ∠BMD= π/3 => ∠AME= π/3
•∠MBF= π/6 and ∠BFM = π/2 => ∠BMF= π/3
•=>ΔBFM is congruent to ΔBDM
•M on BE => ∠BMF + ∠FMA + ∠AME= π
•∠BMF= π/3 and ∠AME= π/3 => ∠FMA= π/3
•∠FMA= π/3 and ∠AFM= π/2 =>ΔBFM is congruent to ΔAFM
•=>FB=FA
•=> F is the perpendicular bisector of AB
Therefore, AD, BE and FG are concurrent at M