From Gogeometry
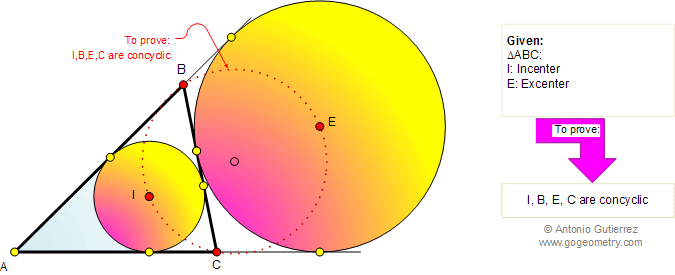

Using
- central and inscribed angle
- congruent triangles
- Concyclic points
- Tangents to a circle
- Inscribed angle and tangent to a circle
- Inradius in right triangle

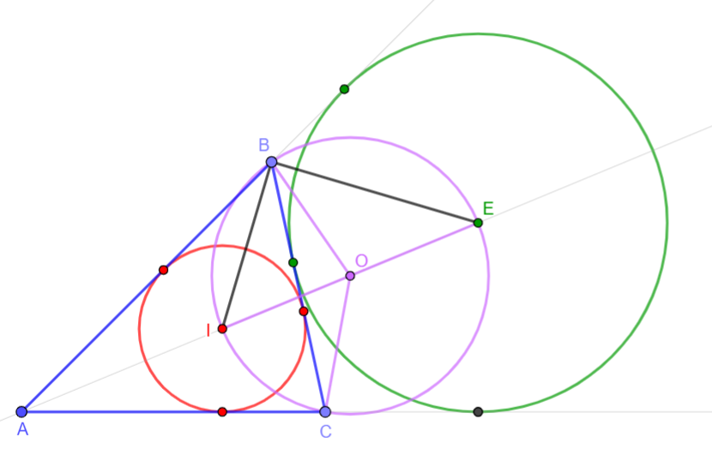
•Point I is on the intersection of the internal angle bisector
•=> AI and IB are internal angle bisector
•Point O is on the intersection of one internal angle bisector and two external angle bisector
•=> AI is an internal angle bisector and BE is an external angle bisector
•=> A, I and E are colinear
•the internal bisector of an angle is perpendicular to its external bisector
•=> IB ⊥ BE
•=>ΔIBE is right in B => I, B and E are on a circle with the center O in the middle of IE and radius r=OE=OB=OI
•The same for I, C and E
•=> I, C and E are on a circle with the center O in the middle of IE and radius r=OE=OC=OI
•That means I, B, E and C are on the same circle with center I and radius r=IE/2